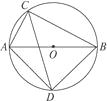
【题目】如图24-1-4-16所示,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=.
参考答案:
【答案】90°
【解析】∠1所对的弧是弧AE,∠2所对的弧是弧BE , 而弧AE+弧BE=弧AB是半圆,因此连结AD , ∠ADB的度数是90°,所以∠ADB=∠1+∠2.本题也可以连结EO , 得到圆心角∠EOA和∠EOB,而∠EOA+∠EOB=180°,所以∠1+∠2=90°.
【考点精析】关于本题考查的等边三角形的性质和圆周角定理,需要了解等边三角形的三个角都相等并且每个角都是60°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象如右图所示,则结论:
的图象如右图所示,则结论:①两函数图象的交点
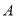 的坐标为
的坐标为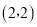 ; ②当
; ②当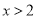 时,
时,  ;
;③当
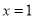 时,
时, 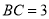 ; ④当
; ④当 逐渐增大时,
逐渐增大时, 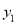 随着
随着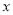 的增大而增大,
的增大而增大, 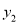 随着
随着 的增大而减小.
的增大而减小.其中正确结论的序号是 .
【答案】①③④
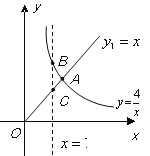
【解析】试题分析:反比例函数与一次函数的交点问题.运用一次函数和反比例函数的性质来解决的一道常见的数形结合的函数试题.一次函数和反比例函数的交点坐标就是一次函数与反比例函数组成的方程组的解.根据k>0确定一次函数和反比例函数在第一象限的图象特征来确定其增减性;根据x=1时求出点B点C的坐标从而求出BC的值;当x=2时两个函数的函数值相等时根据图象求得x>2时y1>y2.
试题解析:①由一次函数与反比例函数的解析式
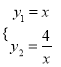 ,
,解得,
 ,
,∴A(2,2),故①正确;
②由图象得x>2时,y1>y2;故②错误;
③当x=1时,B(1,3),C(1,1),∴BC=3,故③正确;
④一次函数是增函数,y随x的增大而增大,反比例函数k>0,y随x的增大而减小.故④正确.
∴①③④正确.
考点:反比例函数与一次函数的交点问题.
【题型】填空题
【结束】
15【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点
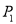 、
、 在函数
在函数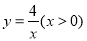 的图象上,斜边
的图象上,斜边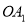 、
、 都在
都在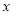 轴上,则点
轴上,则点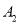 的坐标是____________.
的坐标是____________.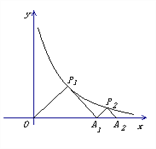
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合中:
-3.1,3.1415,-
 ,+31,0.618,-
,+31,0.618,-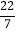 ,0,-1,-(-3).
,0,-1,-(-3).正数集合:{ …};
整数集合:{ …};
负数集合:{ …};
负分数集合:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-24×
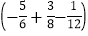 ;
;(2)-9+5×(-6)-(-4)2÷(-8);
(3)0.25×(-2)2-[4÷
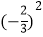 +1]+(-1)2018;
+1]+(-1)2018;(4)-42÷
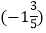 -[
-[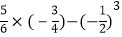 ].
]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点
 、
、 在函数
在函数 的图象上,斜边
的图象上,斜边 、
、 都在
都在 轴上,则点
轴上,则点 的坐标是____________.
的坐标是____________.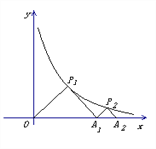
【答案】(
 ,0)
,0)【解析】因为△P1OA1是等腰直角三角形,所以设P1(a,a),则a2=4,a=2,所以OA1=2×2=4,又因为△P2A1A2是等腰直角三角形,设P2(4+b,b),所以b(4+b)=4,解得b=
 ,所以A1A2=
,所以A1A2= ,所以OA2=
,所以OA2= +4=
+4=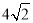 ,则A2(
,则A2( ,0),故答案为(
,0),故答案为( ,0).
,0).【题型】填空题
【结束】
16【题目】如图,函数y=
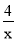 和y=
和y= 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
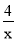 和y=
和y=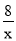 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________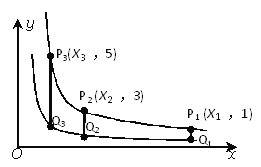
【答案】
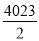
【解析】由题意得,P2012(x2012,4023),因为点P2012在y=
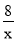 的图象上,所以x2012=
的图象上,所以x2012=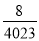 ,把x2012=
,把x2012=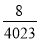 代入 y=
代入 y=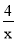 中得y2012=
中得y2012=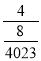 =
=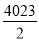 ,故答案为
,故答案为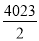 .
.【题型】填空题
【结束】
17【题目】已知y是x的反比例函数,且当x=-4时,y=
 ,
,(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O中,AB为直径,AB=10 cm,弦AC=6 cm,∠ACB的平分线交⊙O于D , 求BC、AD和BD的长.
相关试题

