【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,在
,在![]() 上截取
上截取![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,则
,则![]() ____________.
____________.
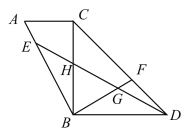
参考答案:
【答案】![]()
【解析】
过点D作DM⊥BD,与BF延长线交于点M,先证明△BHE≌△BGD得到∠EHB=∠DGB,再由平行和对顶角相等得到∠MDG=∠MGD,即MD=MG,在△△BDM中利用勾股定理算出MG的长度,得到BM,再证明△ABC≌△MBD,从而得出BM=AB即可.
解:∵AC∥BD,∠ACB=90°,
∴∠CBD=90°,即∠1+∠2=90°,
又∵BF⊥AB,
∴∠ABF=90°,
即∠8+∠2=90°,
∵BE=BD,
∴∠8=∠1,
在△BHE和△BGD中,
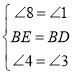 ,
,
∴△BHE≌△BGD(ASA),
∴∠EHB=∠DGB
∴∠5=∠6,∠6=∠7,
∵MD⊥BD
∴∠BDM=90°,
∴BC∥MD,
∴∠5=∠MDG,
∴∠7=∠MDG
∴MG=MD,
∵BC=7,BG=4,
设MG=x,在△BDM中,
BD2+MD2=BM2,
即![]() ,
,
解得x=![]() ,
,
在△ABC和△MBD中
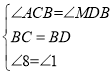 ,
,
∴△ABC≌△MBD(ASA)
AB=BM=BG+MG=4+![]() =
=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目
选手
服装
普通话
主题
演讲技巧
李明
85
70
80
85
张华
90
75
75
80
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
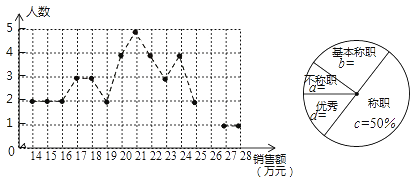
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当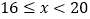 时为“基本称职”,当
时为“基本称职”,当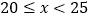 时为“称职”,当
时为“称职”,当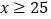 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题: (1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=
 (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市教育行政部门为了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)请你根据图中的信息,回答下列问题:
(1)该校初二学生总人数为____________,扇形统计图中的
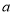 的值为____________,扇形统计图中“活动时间为4天”的扇形所对圆心角度数为______________;
的值为____________,扇形统计图中“活动时间为4天”的扇形所对圆心角度数为______________;(2)请把条形统计图补充完整.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小区有一块四边形空地
 ,其中
,其中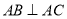 .为响应沙区创文,美化小区的号召,小区计划将这块四边形空地进行规划整理.过点
.为响应沙区创文,美化小区的号召,小区计划将这块四边形空地进行规划整理.过点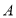 作了垂直于
作了垂直于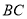 的小路
的小路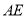 .经测量,
.经测量,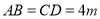 ,
,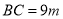 ,
,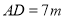 .
.(1)求这块空地
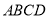 的面积;
的面积;(2)求小路
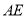 的长.(答案可含根号)
的长.(答案可含根号)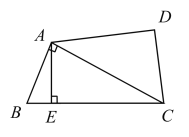
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意一个三位数
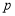 ,将它任意两个数位上的数字对调后得到一个首位不为0的新的三位数
,将它任意两个数位上的数字对调后得到一个首位不为0的新的三位数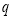 (
(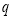 可以与
可以与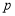 相同),记
相同),记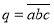 ,在所有可能的情况中,当
,在所有可能的情况中,当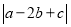 最小时,我们称此时的
最小时,我们称此时的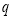 是
是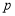 的“平安快乐数”,并规定
的“平安快乐数”,并规定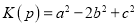 .例如:318按上述方法可得新数381、813、138,因为
.例如:318按上述方法可得新数381、813、138,因为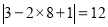 ,
,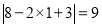 ,
,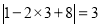 ,而
,而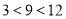 ,所以138是318的“平安快乐数”,此时
,所以138是318的“平安快乐数”,此时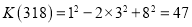 .
.(1)168的“平安快乐数”为_______________,
 ______________;
______________;(2)若
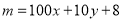 (
( ,
,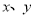 都是正整数),交换其十位与百位上的数字得到新数
都是正整数),交换其十位与百位上的数字得到新数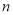 ,当
,当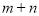 是13的倍数时,求
是13的倍数时,求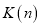 的最大值.
的最大值.
相关试题

