【题目】已知二次函数y=﹣2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
参考答案:
【答案】
(1)解:由题意抛物线的顶点坐标(3,8),
∴抛物线的解析式为y=﹣2(x﹣3)2+8=﹣2x2+12x﹣10,
∴b=12,c=﹣10,
∴b+2c+8=12﹣20+8=0,
∴不等式b+2c+8≥0成立
(2)解:设M(m,n),
由题意 ![]() 3|n|=9,
3|n|=9,
∴n=±6,
①当n=6时,6=﹣2m2+12m﹣10,
解得m=2或4,
②当n=﹣6时,﹣6=﹣2m2+12m﹣10,
解得m=3± ![]() ,
,
∴满足条件的点M的坐标为(2,6)或(4,6)或(3+ ![]() ,﹣6)或(3﹣
,﹣6)或(3﹣ ![]() ,﹣6)
,﹣6)
【解析】由题意可知抛物线的解析式为y=-2(x-3)2+8,由此求出b、c即可解决问题.设M(m,n),由题意![]() 3|n|=9,可得n=±6,分两种情形列出方程求出m的值即可;
3|n|=9,可得n=±6,分两种情形列出方程求出m的值即可;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
(1)如图1,若MP⊥CD,则∠BMP=___度;
(2)如图2,当P点在CD延长线上时,∠BMP=___(用α表示);
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 .

-
科目: 来源: 题型:
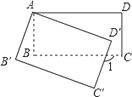
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直径为1的圆从原点沿数轴向左滚动一周,圆上与原点重合的点O到达O′,设点O′表示的数为a.
(1)求a的值;
(2)求﹣(a﹣
 )﹣π的算术平方根.
)﹣π的算术平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD,点E在CD上,连接AE,BD,点G是AE中点,过点G作FH⊥AE,FH分别交AD,BC于点F,H,FH与BD交于点K,且HK=2FG,若EG=
 ,则线段AF的长为_______________.
,则线段AF的长为_______________.
相关试题

