【题目】已知:如图:在△ABC中,∠B=90°,∠A=30°,BC=5cm,等腰Rt△DEF中,∠FDE=![]() ,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
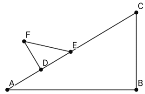
(1)在Rt△DEF沿AC方向移动的过程中,F,C两点之间的距离逐渐_______。(填“不变“变大”或“变小”)
(2)当F、C连线与AB平行时,求AD的长。
(3)以线段AD、FC、BC的长度为三边长的三角形是直角三角形时,求AD的长
参考答案:
【答案】(1)变小;(2)![]() ;(3)AD=6.7cm或4.2cm.
;(3)AD=6.7cm或4.2cm.
【解析】
(1)根据题意可知:DF=3cm,DC逐渐变小,再根据勾股定理即可判断;
(2)根据30°所对的直角边是斜边的一半和平行线的性质,可得:AC=2BC=10cm,∠FCD=∠A=30°,再根据锐角三角函数求出CD,从而求出AD;
(3)设AD=x,根据题意可知:0<x≤10-3=7,则CD= AC-AD=10-x,再根据勾股定理可得:FC=![]() ,然后根据直角三角形斜边的情况分类讨论,最后利用勾股定理分别求出每种情况中x的值即可.
,然后根据直角三角形斜边的情况分类讨论,最后利用勾股定理分别求出每种情况中x的值即可.
解:(1)根据题意可知:DF=DE=3cm,DC逐渐变小,
根据勾股定理可得:FC=![]()
∴F,C两点之间的距离逐渐变小,
故答案为:变小;
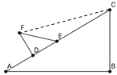
(2)如下图所示,FC∥AB
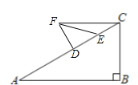
∵∠B=90°,∠A=30°,BC=5cm,
∴AC=2BC=10cm,∠FCD=∠A=30°
在Rt△CFD中,CD=![]() cm
cm
∴AD=AC-CD=![]() ;
;
(3)设AD=x,根据题意可知:0<x≤10-3=7,则CD= AC-AD=10-x
根据勾股定理可得:FC=![]()
①若AD为斜边时,
∴AD2=FC2+BC2
∴![]()
解得:![]() ;
;
②若FC为斜边时,
∴FC2= AD2 +BC2
∴![]()
解得:![]() ;
;
③若BC为斜边时,
∴BC2= AD2 + FC2
∴![]()
整理得:![]()
∵![]()
∴此方程无解.
综上所述:AD=6.7cm或4.2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从A地前往相距5千米的B地,甲骑自行车,途中修车耽误了20分钟,甲行驶的路程s(千米)关于时间t(分钟)的函数图像如图所示;乙慢跑所行的路程s(千米)关于时间t(分钟)的函数解析式为
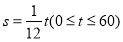
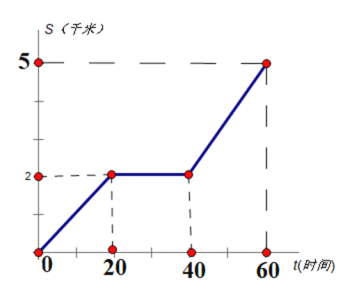
(1)在图中画出乙慢跑所行的路程关于时间的函数图像:
(2)甲修车后行驶的速度是每分钟_______米;
(3)甲、乙两人在出发后,中途_________分钟时相遇
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知正比例函数图像经过点A(2,3)、B(m,6).
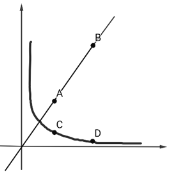
(1)求正比例函数的解析式.
(2)求m的值及A、B两点之间的距离。
(3)分别过点A与点B作y轴的平行线,与反比例函数在第一象限内的分支分别交于点C、D(点C、D均在点A、B下方),若BD=5AC.求反比例函数的解析式,并求出四边形ACDB的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在双曲线y=
 (x>0)上,点C在双曲线y=
(x>0)上,点C在双曲线y= (x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )
(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )
A.
 B. 2
B. 2 C. 4 D. 3
C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=
 (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
(k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
A. 5 B. 10 C. 15 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=
 上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
A. (2,6) B. (3,4) C. (4,3) D. (6,2)
相关试题

