【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

参考答案:
【答案】(1)10;(2)![]()
【解析】
(1)在△BCD中,由勾股定理逆定理可得△BCD是直角三角形,即∠ADB=90°,直角三角形斜边上的中线等于斜边的一半可解得线段DE的长;
(2) 当DE⊥AB时,DE有最小值.根据等面积法即可求出DE的长.
解:(1)∵AC=21,AD=16,
∴CD=21-16=5,
∵DC +BD =5 +12 =169,BC =13 =169,
∴DC +BD = BC ,
∴△BCD是直角三角形。且∠BDC=90°,
∴∠ADB=90°,
在Rt△ADB中,由勾股定理得AB=![]() =20,
=20,
∵∠ADB=90°,E为斜边AB的中点,
∴DE=![]() AB=
AB=![]() ×20=10.
×20=10.
(2)当DE⊥AB时,DE有最小值.
此时AB×DE=AD×DB,即20DE=16×12,
解得DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,E,F分别在边AC、BC上,满足AE=CF,连接BE,AF交于点P.
(1)求证:△ABE≌△CAF;
(2)求∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )

A.70°
B.35°
C.40°
D.50° -
科目: 来源: 题型:
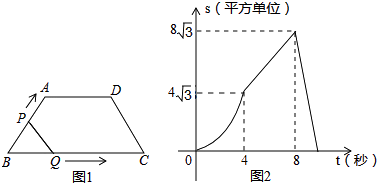
查看答案和解析>>【题目】如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的是( )
A.当t=4秒时,S=4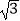
B.AD=4
C.当4≤t≤8时,S=2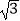 t
t
D.当t=9秒时,BP平分梯形ABCD的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根为x1和x2 , 且(x1﹣2)(x1﹣x2)=0,则k的值是 .
-
科目: 来源: 题型:
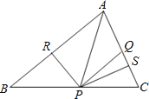
查看答案和解析>>【题目】如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
相关试题

