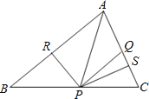
【题目】如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
参考答案:
【答案】(1)证明见解析;(2)相等,理由见解析.
【解析】
(1)易证RT△APR≌RT△APS,可得∠BAP=∠1,再根据AQ=PQ,可得∠1=∠2,即可求得QP∥AR;
(2) 根据HL证明Rt△APR≌Rt△APS,即可推出AS=AR.
解:(1)如图,
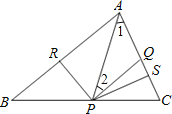
在RT△APR和RT△APS中,
![]() ,
,
∴RT△APR≌RT△APS(HL),
∴∠BAP=∠1,
∵AQ=PQ,
∴∠1=∠2,
∴∠BAP=∠2,
∴QP∥AR.
(2)AR=AS,理由如下:
∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
![]() ,
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的是( )
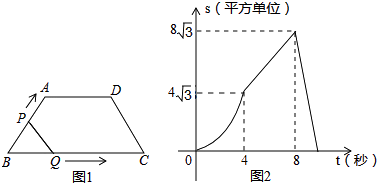
A.当t=4秒时,S=4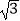
B.AD=4
C.当4≤t≤8时,S=2 t
t
D.当t=9秒时,BP平分梯形ABCD的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根为x1和x2 , 且(x1﹣2)(x1﹣x2)=0,则k的值是 .
-
科目: 来源: 题型:
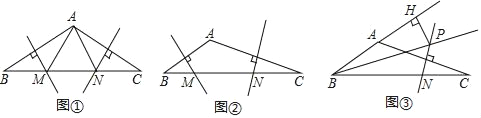
查看答案和解析>>【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题探究)
(1)如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系_____________ ;(不必证明)
(深入探究)
(2)如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段 BC,DC,EC 之间满足的等量关系式为________________ ;(不必证明) 线段 AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(拓展应用)
(3)如图③,在四边形 ABCD 中,∠ABC=∠ACB=∠ADC=45°.若 BD=9,CD=3,
求 AD 的长.

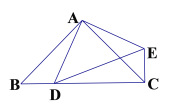

① ② ③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根为x1和x2 , 且(x1﹣2)(x1﹣x2)=0,则k的值是 .
相关试题

