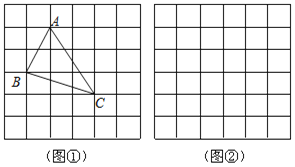
【题目】如图①,在正方形网格中,每个小正方形的边长为1.在网格中构造格点△ABC(即△ABC 三个顶点都在小正方形的顶点处),AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,利用网格就能计算三角形的面积.
,利用网格就能计算三角形的面积.
(1)请你将△ABC的面积直接填写在横线上.
(2)在图②中画出△DEF,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]() .
.
①判断三角形的形状,说明理由.
②求这个三角形的面积.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用“构图法”求解△ABC的面积即可.
(2)根据网格结构与勾股定理确定出点D、E、F,顺次连接可得△DEF,利用勾股定理的逆定理,可判断是直角三角形,代入面积公式可求出面积.
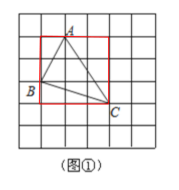
解:(1)S△ABC=3×3-![]() ×1×2-
×1×2-![]() ×2×3-
×2×3-![]() ×1×3=
×1×3=![]() ,
,
(2)如图所示,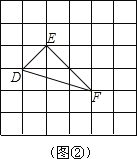 .
.
①△DEF为直角三角形,
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴△DEF为直角三角形,
②S△DEF=![]() DE×EF=
DE×EF=![]() ×
×![]() ×2
×2![]() =2.
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )
A.有最大值
B.有最大值﹣
C.有最小值
D.有最小值﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的例题,再解答后面的题目.
例:已知x2+y2﹣2x+4y+5=0,求x+y的值.
解:由已知得(x2﹣2x+1)+(y2+4y+4)=0,
即(x﹣1)2+(y+2)2=0.
因为(x﹣1)2≥0,(y+2)2≥0,它们的和为0,
所以必有(x﹣1)2=0,(y+2)2=0,
所以x=1,y=﹣2.
所以x+y=﹣1.
题目:已知x2+4y2﹣6x+4y+10=0,求xy的值.
-
科目: 来源: 题型:
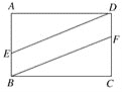
查看答案和解析>>【题目】如图,长方形ABCD表示一块草地,点E,F分别在边AB、CD上,BF∥DE,四边形EBFD是一条水泥小路,若AD=12米,AB=7米,且AE∶EB=5∶2,求草地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD∥BC,AB∥CD,BE平分∠ABC,EC平分∠BED,∠ECD=45°,则∠ABC的度数为( )

A.45°B.52°C.56°D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠A=60°,BD、BE三等分∠ABC,CD、CE三等分∠ACB,连接DE,则∠BDE=_____________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,
 的三个顶点的坐标分别
的三个顶点的坐标分别 

(1)画出 关于
关于  轴的对称图形
轴的对称图形  ;
;
(2)画出将 绕原点
绕原点  逆时针方向旋转
逆时针方向旋转  得到的
得到的 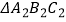 ;
;
(3)求(2)中线段 扫过的图形面积.
扫过的图形面积.
相关试题

