【题目】若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )
A.有最大值 ![]()
B.有最大值﹣ ![]()
C.有最小值 ![]()
D.有最小值﹣ ![]()
参考答案:
【答案】B
【解析】解:∵一次函数y=(m+1)x+m的图象过第一、三、四象限,
∴m+1>0,m<0,
即﹣1<m<0,
∴函数y=mx2﹣mx=m(x﹣ ![]() )2﹣
)2﹣ ![]() 有最大值,
有最大值,
∴最大值为﹣ ![]() .
.
故选B.
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识,掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远,以及对二次函数的最值的理解,了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
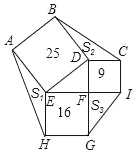
查看答案和解析>>【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副直角三角板叠放在一起可以拼出多种图形,如图①—④,每幅图中所求角度正确的个数有( )
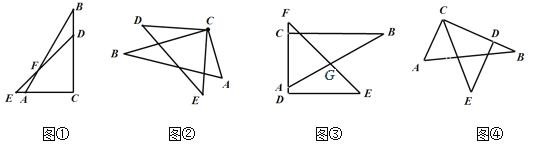
①∠BFD=15°;②∠ACD+∠ECB=150°;③∠BGE=45° ;④∠ACE=30°
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的例题,再解答后面的题目.
例:已知x2+y2﹣2x+4y+5=0,求x+y的值.
解:由已知得(x2﹣2x+1)+(y2+4y+4)=0,
即(x﹣1)2+(y+2)2=0.
因为(x﹣1)2≥0,(y+2)2≥0,它们的和为0,
所以必有(x﹣1)2=0,(y+2)2=0,
所以x=1,y=﹣2.
所以x+y=﹣1.
题目:已知x2+4y2﹣6x+4y+10=0,求xy的值.
-
科目: 来源: 题型:
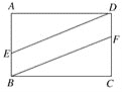
查看答案和解析>>【题目】如图,长方形ABCD表示一块草地,点E,F分别在边AB、CD上,BF∥DE,四边形EBFD是一条水泥小路,若AD=12米,AB=7米,且AE∶EB=5∶2,求草地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形网格中,每个小正方形的边长为1.在网格中构造格点△ABC(即△ABC 三个顶点都在小正方形的顶点处),AB、BC、AC三边的长分别为
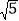 、
、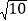 、
、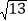 ,利用网格就能计算三角形的面积.
,利用网格就能计算三角形的面积.(1)请你将△ABC的面积直接填写在横线上.
(2)在图②中画出△DEF,DE、EF、DF三边的长分别为
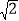 、
、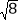 、
、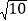 .
.①判断三角形的形状,说明理由.
②求这个三角形的面积.
相关试题

