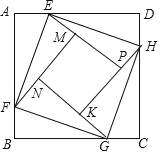
【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A. 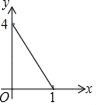 B.
B. 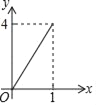 C.
C.  D.
D. 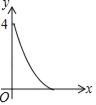
参考答案:
【答案】D
【解析】根据题意和图形,由AE=x(0<x<1),S四边形MNKP=y,得出y=S正方形ABCD-2(S△AEF+S△BGF+S△CGH+S△DEH)2×2﹣2×[![]() x(2﹣x)+
x(2﹣x)+![]() x(2﹣x)+
x(2﹣x)+![]() x(2﹣x)+
x(2﹣x)+![]() x(2﹣x)]=4x2﹣8x+4=4(x﹣1)2,然后根据0<x<1,可得到0<y<4,最后知此函数是二次函数,开口向上,即图象是抛物线,即选项A、B、C错误;选项D符合.
x(2﹣x)]=4x2﹣8x+4=4(x﹣1)2,然后根据0<x<1,可得到0<y<4,最后知此函数是二次函数,开口向上,即图象是抛物线,即选项A、B、C错误;选项D符合.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为打造智慧课堂,准备集体购买一批平板电脑,原计划订购60台,每台1000元,商家表示,如果多购,可以优惠,结果校长实际订购了72台,每台减价30元,但商家获得同样多的利润.
(1)求每台平板电脑的成本是多少元?
(2)求商家的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )种
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)图中的t1= 分;
(2)若乙提速后,乙登山的速度是甲登山的速度的3倍,
①则甲登山的速度是 米/分,图中的t2= 分;
②请求出乙登山过程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
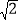 ,将△ABC绕点A顺时针方向旋转60°到
,将△ABC绕点A顺时针方向旋转60°到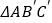 的位置,连接
的位置,连接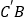 ,则
,则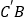 的长为( ).
的长为( ).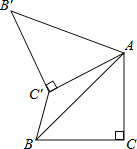
A.
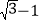 B.
B.  C.
C. 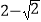 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有
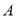 、
、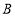 两点,分别代表-12、4.
两点,分别代表-12、4.(1)
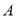 、
、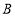 两点间的距离为 个单位长度;
两点间的距离为 个单位长度;(2)点
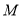 从点
从点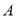 出发,以1个单位长度秒的速度沿数轴向点
出发,以1个单位长度秒的速度沿数轴向点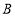 做匀速运动,同时点
做匀速运动,同时点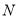 从点
从点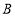 出发,以3个单位长度/秒的速度沿数轴由
出发,以3个单位长度/秒的速度沿数轴由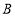 →
→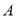 →
→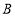 的路径做匀速运动,当点
的路径做匀速运动,当点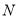 最后到达
最后到达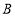 点时,都停止运动.设运动时间为
点时,都停止运动.设运动时间为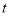 秒
秒①请写出
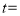 时,
时,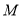 、
、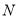 两点相遇.
两点相遇.②当
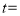 时,两点停止运动.
时,两点停止运动.③当
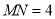 时,求
时,求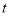 的值.
的值.
相关试题

