【题目】已知数轴上有![]() 、
、![]() 两点,分别代表-12、4.
两点,分别代表-12、4.
(1) ![]() 、
、![]() 两点间的距离为 个单位长度;
两点间的距离为 个单位长度;
(2)点![]() 从点
从点![]() 出发,以1个单位长度秒的速度沿数轴向点
出发,以1个单位长度秒的速度沿数轴向点![]() 做匀速运动,同时点
做匀速运动,同时点![]() 从点
从点![]() 出发,以3个单位长度/秒的速度沿数轴由
出发,以3个单位长度/秒的速度沿数轴由![]() →
→![]() →
→![]() 的路径做匀速运动,当点
的路径做匀速运动,当点![]() 最后到达
最后到达![]() 点时,都停止运动.设运动时间为
点时,都停止运动.设运动时间为![]() 秒
秒
①请写出![]() 时,
时,![]() 、
、![]() 两点相遇.
两点相遇.
②当![]() 时,两点停止运动.
时,两点停止运动.
③当![]() 时,求
时,求![]() 的值.
的值.
![]()
参考答案:
【答案】(1)16;(2)①当![]() 或
或![]() 时,它们相遇;②当
时,它们相遇;②当![]() 时,两点停止运动;③当
时,两点停止运动;③当![]() 时,求
时,求![]() 的值为4或5或6或10.
的值为4或5或6或10.
【解析】
(1)根据![]() 、
、![]() 两点间的距离等于它们表示的数的差的绝对值计算即可;
两点间的距离等于它们表示的数的差的绝对值计算即可;
(2)①分N未到A点时相遇和N到达A点返回时相遇两种情况,列出方程求解即可;
②停止时N所走的路程为2×AB,用路程除以速度即可求得时间;
(3)分M、N相遇前,M、N第一次相遇后N未到达A点和当N已经从A点返回M、N第二次相遇前,M、N第二次相遇后四种情况讨论,列出方程求解即可;
解:(1)![]() 、
、![]() 两点间的距离为AB=|4-(-12)|=16.
两点间的距离为AB=|4-(-12)|=16.
故答案为16;
(2)①当N未走到A点时它们相遇,此时根据题意
![]() ,解得
,解得![]() ,
,
当N到达A点返回时它们相遇,此时根据题意
![]() ,解得
,解得![]() ,
,
故当![]() 或
或![]() 时,它们相遇;
时,它们相遇;
②根据当点![]() 最后到达
最后到达![]() 点时,都停止运动,
点时,都停止运动,
![]() ,
,
故当![]() 时,两点停止运动;
时,两点停止运动;
③当M、N相遇前,![]() 时,根据题意
时,根据题意
![]() ,解得
,解得![]() ,
,
当M、N第一次相遇后,但N还未到达A点,![]() 时,根据题意
时,根据题意
![]() ,解得
,解得![]() ,
,
当N已经从A点返回,M、N第二次相遇前,![]() 时,根据题意
时,根据题意
![]() ,解得
,解得![]() ,
,
当N已经从A点返回,M、N第二次相遇后,![]() 时,根据题意
时,根据题意
![]() ,解得
,解得![]() ,
,
综上所述,当![]() 时,求
时,求![]() 的值为4或5或6或10.
的值为4或5或6或10.
-
科目: 来源: 题型:
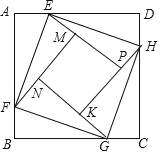
查看答案和解析>>【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A.
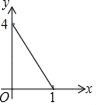 B.
B. 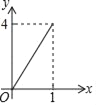 C.
C.  D.
D. 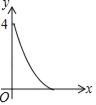
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
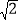 ,将△ABC绕点A顺时针方向旋转60°到
,将△ABC绕点A顺时针方向旋转60°到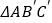 的位置,连接
的位置,连接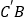 ,则
,则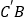 的长为( ).
的长为( ).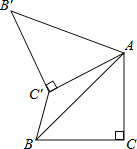
A.
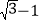 B.
B.  C.
C. 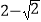 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了解高峰时段从总站乘16路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:
14,23,16,25,23,28,26,27,23,25.
(1)计算这10个班次乘车人数的平均数;
(2)如果16路车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2
 ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某同学在沙滩上用石头摆成的小房子观察规律变化,写出第⑧个小房子用了_____块石头.

相关试题

