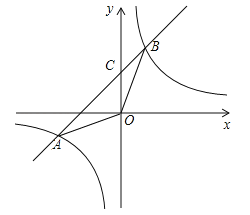
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.

参考答案:
【答案】(1)![]() ,y=x+2;(2)C(0,2),6.
,y=x+2;(2)C(0,2),6.
【解析】
试题分析:(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,从而得出反比例函数表达式,再由点B的坐标和反比例函数表达式即可求出m值,结合点A、B的坐标利用待定系数法即可求出一次函数表达式;
(2)令一次函数表达式中x=0求出y值即可得出点C的坐标,利用分解图形求面积法结合点A、B的坐标即可得出结论.
试题解析:(1)∵点A(﹣4,﹣2)在反比例函数![]() 的图象上,∴k=﹣4×(﹣2)=8,∴反比例函数的表达式为
的图象上,∴k=﹣4×(﹣2)=8,∴反比例函数的表达式为![]() ;
;
∵点B(m,4)在反比例函数![]() 的图象上,∴4m=8,解得:m=2,∴点B(2,4).
的图象上,∴4m=8,解得:m=2,∴点B(2,4).
将点A(﹣4,﹣2)、B(2,4)代入y=﹣ax+b中,得:![]() ,解得:
,解得:![]() ,∴一次函数的表达式为y=x+2.
,∴一次函数的表达式为y=x+2.
(2)令y=x+2中x=0,则y=2,∴点C的坐标为(0,2),∴S△AOB=![]() OC×(xB﹣xA)=
OC×(xB﹣xA)=![]() ×2×[2﹣(﹣4)]=6.
×2×[2﹣(﹣4)]=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(8分)

(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 .
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 .
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B,点A在点B的左边,点A表示的数为a,点B表示的数为b,且A、B两点的距离是8.
(1)点A与点B之间(包括A、B两点)的整数有__________个;
(2)当a=-3时,b=_______;
(3)当
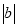 =5时,a=__________;
=5时,a=__________;(4)当a取何值时,
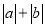 的值最小?最小值是多少?
的值最小?最小值是多少?(5)若
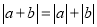 ,求a的范围.
,求a的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2+x向下平移2个单位,所得抛物线的表达式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是方程x2﹣x﹣1=0的两根,则x12+x22的值是( )
A. 3 B. 1 C. ﹣1 D. ﹣3
-
科目: 来源: 题型:
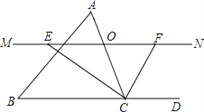
查看答案和解析>>【题目】如图,在△ABC中,点O是边AC上一个动点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动到什么位置,四边形AECF是矩形,请说明理由;
(3)在第(2)问的基础上,△ABC满足什么条件时,四边形AECF是正方形?(不需说明理由)
(4)当点O在边AC上运动时,四边形BCFE能成为菱形吗?若能,请加以证明;若不能,则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.在-6、-2、0、3这四个数中,最小的数是__________.
相关试题

