【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(8分)

(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 .
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 .
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
参考答案:
【答案】(1)无理;-π;(2)±4π;(3)①第4次;第3次;②26π;-6π .
【解析】
试题分析:(1)利用圆的半径以及滚动周数即可得出滚动距离;(2)利用圆的半径以及滚动周数即可得出滚动距离,注意两个方向;(3)①利用滚动的方向以及滚动的周数即可得出A点移动距离变化;②利用绝对值的性质以及有理数的加减运算得出移动距离和A表示的数即可.
试题解析:(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C到原点的距离是半圆周长,圆半径为1,所以点C表示的数是无理数,这个数是-π;故答案为:无理,-π;(2)把圆片沿数轴滚动2周,向左或向右,点A到达数轴上点D的位置,点D到原点的距离是两个圆周长,半径还是1,故点D表示的数是4π或-4π;故答案为:4π或-4π;(3)①∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3,因为(+2)+(-1)+(+3)+(-4)=0,∴第4次滚动后,A点距离原点最近,因为(+2)+(-1)+(+3)=4,所以第3次滚动后,A点距离原点最远;②∵A点运动的圆周数为:|+2|+|-1|+|+3|+|-4|+|-3|=13,∴13×2π×1=26π,∴A点运动的路程共有26π;∵(+2)+(-1)+(+3)+(-4)+(-3)=-3,(-3)×2π=-6π,∴此时点A所表示的数是:-6π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列各数:
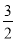 , -4, 3.5, -1.5, 0, 2,
, -4, 3.5, -1.5, 0, 2, 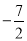 ,
, (1)在这些数中,整数是 ;负分数是 。
(2)在数轴上表示出这些数,并指出与原点距离最远的数是 。
(3)把这些数用“<”连接起来。
-
科目: 来源: 题型:
查看答案和解析>>【题目】+8与互为相反数,请赋予它实际意义: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国最新研制的巨型计算机“曙光3000超级服务器”,它的运算峰值可以达到每秒403200000000次.这个数字用科学记数法来表示( )
A.4032×108
B.4.032×1010
C.4.032×1011
D.4.032×1012 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B,点A在点B的左边,点A表示的数为a,点B表示的数为b,且A、B两点的距离是8.
(1)点A与点B之间(包括A、B两点)的整数有__________个;
(2)当a=-3时,b=_______;
(3)当
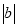 =5时,a=__________;
=5时,a=__________;(4)当a取何值时,
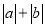 的值最小?最小值是多少?
的值最小?最小值是多少?(5)若
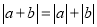 ,求a的范围.
,求a的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2+x向下平移2个单位,所得抛物线的表达式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数
 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.

相关试题

