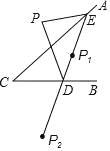
【题目】如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为_____.
参考答案:
【答案】4.5
【解析】
利用轴对称图形的性质得出PE=EP1,PD=DP2,进而利用DE=4cm,得出P1D的长,即可得出P1P2的长.
∵点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,
∴PE=EP1,PD=DP2,
∵PE=2.5cm,PD=3cm,DE=4cm,
∴P2D=3cm,EP1=2.5cm,
即DP1=DEEP1=42.5=1.5(cm),
则线段P1P2的长为:P1D+DP2=1.5+3=4.5(cm).
故答案为4.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理
 、
、 两种型号的净水器,每台
两种型号的净水器,每台 型净水器比每台
型净水器比每台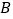 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进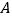 型净水器与用4.5万元购进
型净水器与用4.5万元购进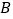 型净水器的数量相等.
型净水器的数量相等.(1)求每台
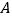 型、
型、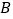 型净水器的进价各是多少元;
型净水器的进价各是多少元;(2)槐荫公司计划购进
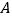 、
、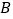 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中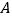 型净水器为
型净水器为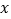 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时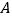 型净水器每台售价2500元,
型净水器每台售价2500元,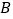 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售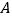 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献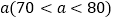 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为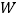 ,求
,求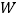 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)[(-3a2b3)3]2;
(2)(-2xy2)6+(-3x2y4)3;
(3)
 ;
; (4)(0.5×3
 )199×(-2×
)199×(-2×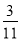 )200.
)200. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
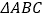 中,
中,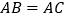 ,以
,以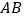 为直径的
为直径的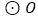 交
交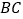 于点
于点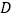 ,交
,交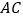 于点
于点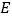 ,过点
,过点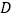 作
作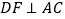 于点
于点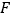 ,交
,交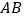 的延长线于点
的延长线于点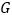 .
.
(1)求证:
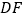 是
是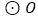 的切线;
的切线;(2)已知
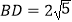 ,
,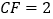 ,求
,求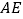 和
和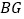 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC,AB=AC,AC的垂直平分线与AB所在直线相交所得的锐角为40°,∠C=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
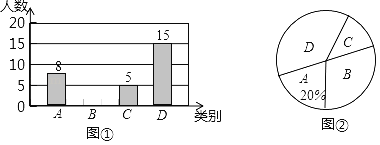
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
相关试题

