【题目】已知函数f(x)= ![]() +
+ ![]() (1﹣a2)x2﹣ax,其中a∈R.
(1﹣a2)x2﹣ax,其中a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为8x+y﹣2=0,求a的值;
(2)当a≠0时,求函数f(x)(x>0)的单调区间与极值;
(3)若a=1,存在实数m,使得方程f(x)=m恰好有三个不同的解,求实数m的取值范围.
参考答案:
【答案】
(1)解:f'(x)=ax2+(1﹣a2)x﹣a,由8x+y﹣2=0可得f'(1)=﹣8,
即f'(1)=a+(1﹣a2)﹣a=﹣8,解得a=±3,
当a=3时,f(x)=x3﹣4x2﹣3x,f(1)=﹣6,f'(x)=3x2﹣8x﹣3,f'(1)=﹣8,
当a=﹣3时,f(x)=﹣x3﹣4x2+3,f(1)=﹣2,f'(x)=﹣3x2﹣8x+3,f'(1)=﹣8,
故曲线y=f(x)在点(1,f(1))处的切线方程为y+2=﹣8(x﹣1),即8x+y﹣6=0不符合题意,舍去,
故a的值为3
(2)解:当a≠0时,f′(x)=ax2+(1﹣a2)x﹣a=(x﹣a)(ax+1)=a(x﹣a)(x+ ![]() ),
),
当a>0时,令f'(x)=0,则 ![]()
当x变化时,f'(x),f(x)的变化情况如下表:
x | (﹣∞,﹣ | ﹣ | (﹣ | a | (a,+∞) |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
∴f(x)的单调递增区间为 ![]() ,单调递减区间为
,单调递减区间为 ![]() .
.
函数f(x)在 ![]() 处取得最大值
处取得最大值 ![]() ,且
,且 ![]() .
.
函数f(x)在x2=a处取得极小值f(a),且 ![]() ,
,
当a<0时,令f'(x)=0,则 ![]() ,
,
当x变化时,f'(x),f(x)的变化情况如下表:
x | (﹣∞,a) | a | (a,﹣ | ﹣ | (﹣ |
f'(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | ↓ | 极小值 | ↑ | 极大值 | ↓ |
∴f(x)的单调递减区间为 ![]() ,单调递增区间为
,单调递增区间为 ![]() ,
,
函数f(x)在 ![]() 处取得极大值
处取得极大值 ![]() ,
,
且 ![]() .
.
函数f(x)在x2=a处取得极小值f(a),且 ![]()
(3)解:若a=1,则 ![]() ,
,
由(2)可知 ![]() 在区间(﹣∞,﹣1),(1,+∞)内增函数,在区间(﹣1,1)内为减函数,
在区间(﹣∞,﹣1),(1,+∞)内增函数,在区间(﹣1,1)内为减函数,
函数f(x)在x1=1处取的极小值f(1),且 ![]() .
.
函数f(x)在x2=﹣1处取得极大值f(﹣1),且 ![]() .
.
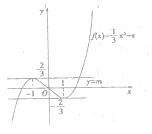
如图分别作出函数 ![]() 与y=m的图象,
与y=m的图象,
从图象上可以看出当 ![]() 时,两个函数的图象有三个不同的交点,
时,两个函数的图象有三个不同的交点,
即方程f(x)=m有三个不同的解,
故实数m的取值范围为 ![]() .
.
【解析】(1)求导,由f'(1)=﹣8,求得a的值,分别求得切线方程,与原切线方程比较,即可求得a的值;(2)求导,根据导数与函数单调性的关系,分类讨论,即可求得函数f(x)(x>0)的单调区间与极值;(3)由(2)可知:根据函数的单调性,求得f(x)的极值,分别作出函数 ![]() 与y=m的图象,从图象上可以看出当
与y=m的图象,从图象上可以看出当 ![]() 时,两个函数的图象有三个不同的交点,即可求得m的取值范围.
时,两个函数的图象有三个不同的交点,即可求得m的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从
 地出发向
地出发向 地行走,同时小聪从
地行走,同时小聪从 地出发向
地出发向 地行走,如图所示,相交于点
地行走,如图所示,相交于点 的两条线段
的两条线段 分别表示小敏、小聪离
分别表示小敏、小聪离 地的距离
地的距离 (km)与已用时间
(km)与已用时间 (h)之间的关系,则
(h)之间的关系,则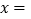 ________时,小敏、小聪两人相距7 km.
________时,小敏、小聪两人相距7 km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且
 .
. 
(1)判断直线EF平面ABCD的位置关系,并说明理由;
(2)若∠CBA=60°,求二面角A﹣FB﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线C由上半椭圆
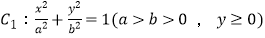 和部分抛物线
和部分抛物线 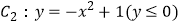 连接而成,C1与C2的公共点为A,B,其中C1的离心率为
连接而成,C1与C2的公共点为A,B,其中C1的离心率为 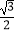 .
.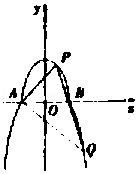
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),是否存在直线l,使得PQ为直径的圆恰好过点A,若存在直线l的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为  .
.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明 为定值,并求△AOB的面积的最大值.
为定值,并求△AOB的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣2|+|2x+a|,a∈R. (Ⅰ)当a=1时,解不等式f(x)≥5;
(Ⅱ)若存在x0满足f(x0)+|x0﹣2|<3,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】
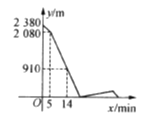
 两地之间的路程为2 380 m,甲、乙两人分别从
两地之间的路程为2 380 m,甲、乙两人分别从 两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在
两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在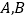 之间的
之间的 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回 地,乙继续向
地,乙继续向 地前行.甲到达
地前行.甲到达 地时停止行走,乙到达
地时停止行走,乙到达 地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程 (m)与甲出发的时间
(m)与甲出发的时间 (min)之间的关系如图所示,则乙到达
(min)之间的关系如图所示,则乙到达 地时,甲与
地时,甲与 地相距的路程是
地相距的路程是________m.
相关试题

