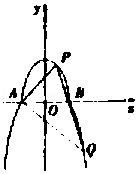
【题目】如图,曲线C由上半椭圆 ![]() 和部分抛物线
和部分抛物线 ![]() 连接而成,C1与C2的公共点为A,B,其中C1的离心率为
连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
.
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),是否存在直线l,使得PQ为直径的圆恰好过点A,若存在直线l的方程;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:在C1,C2的方程中,令y=0,可得b=1,且A(﹣1,0),B(1,0)是上半椭圆C1的左右顶点,
设C1的半焦距为c,由 ![]() 及a2﹣c2=b2﹣1,
及a2﹣c2=b2﹣1,
可得a=2,所以a=2,b=1
(2)
解:由(1),上半椭圆C1的方程为 ![]() ,
,
由题意知,直线l与x轴不重合也不垂直,设其方程为y=k(x﹣1)(k≠0),
代入C1的方程,整理得(k2+4)x2﹣2k2x+k2﹣4=0,
设点P的坐标为(xP,yP),
因为直线l过点B,所以x=1是方程的一个根,
由求根公式,得 ![]() ,所以点P的坐标为
,所以点P的坐标为 ![]() ,
,
同理,由 ![]() ,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),
,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),
所以 ![]() ,
,
依题意可知AP⊥AQ,所以 ![]() ,即
,即 ![]() ,
,
即 ![]() ,
,
因为k≠0,所以k﹣4(k+2)=0,解得 ![]() ,
,
经检验, ![]() 符合题意,故直线l的方程为
符合题意,故直线l的方程为 ![]()
【解析】(1)在C1 , C2的方程中,令y=0,可得b=1,且A(﹣1,0),B(1,0)是上半椭圆C1的左右顶点,设C1的半焦距为c,由 ![]() 及a2﹣c2=b2﹣1,联立解得a.(2)由(1),上半椭圆C1的方程为
及a2﹣c2=b2﹣1,联立解得a.(2)由(1),上半椭圆C1的方程为 ![]() ,由题意知,直线l与x轴不重合也不垂直,设其方程为
,由题意知,直线l与x轴不重合也不垂直,设其方程为
y=k(x﹣1)(k≠0),代入C1的方程,整理得(k2+4)x2﹣2k2x+k2﹣4=0,设点P的坐标为(xP , yP),由求根公式,得点P的坐标为 ![]() ,同理,由
,同理,由 ![]() ,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),依题意可知AP⊥AQ,所以
,得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),依题意可知AP⊥AQ,所以 ![]() ,即可得出k.
,即可得出k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市储运部紧急调拨一批物资,调进物资共用4h,调进物资2h后开始调出物资(调进物资与调出物资的速度探持不变).储运部库存物资
 (t)与时间
(t)与时间 (h)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(h)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
A. 4 h B. 4.4 h C. 4.8 h D. 5 h
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从
 地出发向
地出发向 地行走,同时小聪从
地行走,同时小聪从 地出发向
地出发向 地行走,如图所示,相交于点
地行走,如图所示,相交于点 的两条线段
的两条线段 分别表示小敏、小聪离
分别表示小敏、小聪离 地的距离
地的距离 (km)与已用时间
(km)与已用时间 (h)之间的关系,则
(h)之间的关系,则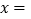 ________时,小敏、小聪两人相距7 km.
________时,小敏、小聪两人相距7 km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且
 .
. 
(1)判断直线EF平面ABCD的位置关系,并说明理由;
(2)若∠CBA=60°,求二面角A﹣FB﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 +
+  (1﹣a2)x2﹣ax,其中a∈R.
(1﹣a2)x2﹣ax,其中a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为8x+y﹣2=0,求a的值;
(2)当a≠0时,求函数f(x)(x>0)的单调区间与极值;
(3)若a=1,存在实数m,使得方程f(x)=m恰好有三个不同的解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为  .
.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明 为定值,并求△AOB的面积的最大值.
为定值,并求△AOB的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣2|+|2x+a|,a∈R. (Ⅰ)当a=1时,解不等式f(x)≥5;
(Ⅱ)若存在x0满足f(x0)+|x0﹣2|<3,求a的取值范围.
相关试题

