Question

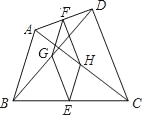
【题目】如图，四边形ABCD中，AB=CD，点E、F、G、H分别是BC、AD、BD、AC的中点，猜想四边形EHFG的形状并说明理由．

Answer 1

【答案】证明见解析

【解析】

首先运用三角形中位线定理可得到FG∥AB，HE∥AB，FH∥CD，GE∥DC，从而在根据平行于同一条直线的两直线平行得到GE∥FH，GF∥EH，可得到四边形GFHE是平行四边形，再运用三角形中位线定理证明邻边相等，从而证明它是菱形．

∵四边形ABCD中，点E、F、G、H分别是BC、AD、BD、AC的中点，

∴FG∥AB，HE∥AB，FH∥CD，GE∥DC，

∴GE∥FH，GF∥EH（平行于同一条直线的两直线平行）；

∴四边形GFHE是平行四边形，

∵四边形ABCD中，点E、F、G、H分别是BC、AD、BD、AC的中点，

∴FG是△ABD的中位线，GE是△BCD的中位线，

∴GF=AB，GE=CD，

∵AB=CD，

∴GF=GE，

∴四边形EHFG是菱形．