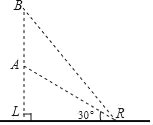
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.
参考答案:
【答案】20![]() -20
-20
【解析】
根据图形,直接利用锐角三角函数的定义得出LR=AR×cos∠ARL,代入数据求出LR的长,接下来,利用锐角三角函数关系得出BL=LR×tan∠BRL,再利用AL=ARsin∠ARL,求出AL的值,进而得出答案.
在Rt△ALR中,AR=40km,∠ARL=30°,
∵cos∠ARL=![]() ,
,
∴LR=AR×cos∠ARL=40×cos30°≈20![]() (km).
(km).
在Rt△BLR中,LR=20![]() km,∠BRL=45°,
km,∠BRL=45°,
∵tan∠BRL=![]() ,
,
∴BL=LR×tan∠BRL=20![]() ×tan45°≈20
×tan45°≈20![]() ×1=20
×1=20![]() (km),
(km),
又∵sin∠ARL=![]() ,
,
∴AL=ARsin∠ARL=40×sin30°=20(km),
∴AB=BL-AL=(20![]() -20)km.
-20)km.
故答案为:(20![]() -20)km.
-20)km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用
 (元)与种植面积
(元)与种植面积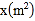 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当
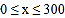 和
和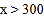 时,
时, 与
与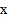 的函数关系式;
的函数关系式;(2)广场上甲、乙两种花卉的种植面积共
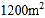 ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于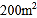 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某县结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见下表
一户居民一个月用电量的范围
电费价格(单位:元/千瓦时)
不超过150千瓦时的部分
a
超过150千瓦时,但不超过230千瓦时的部分
b
超过230千瓦时的部分
a+0.33
2019年10月份,该县居民甲用电100千瓦时,交费64元;居民乙用电200千瓦时,交费134.5元.
(1)根据题意,求出上表中a和b的值;
(2)实行“阶梯电价”收费以后,该县居民当月用电多少千瓦时时,其当月的平均电价为0.67元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P(m,n)是抛物线y=
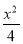 -1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
-1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.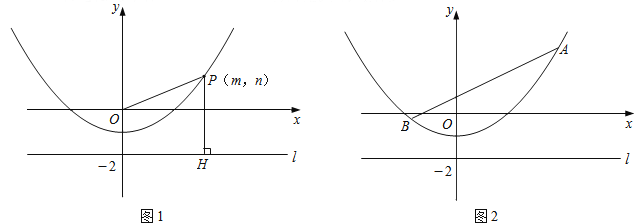
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线y=
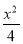 -1上滑动,求A,B两点到直线l的距离之和的最小值.
-1上滑动,求A,B两点到直线l的距离之和的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内.如图,为了测量来雁塔的高度,在E处用高为1.5 m的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4 m,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1 m)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A
 ,B(-1,2)是一次函数
,B(-1,2)是一次函数 与反比例函数
与反比例函数
(
 )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

相关试题

