【题目】如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( ) 
A.![]()
B.3
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:∵△ABC中,∠C=90°,∠A=30°,BC=2, ∴AB=2BC=4.
∵DE是线段AB的垂直平分线,
∴BD=AD= ![]() AB=2,BE=AE,
AB=2,BE=AE,
∴∠ABE=∠A=30°,
∴BE= ![]() =
= ![]() =
= ![]() .
.
故选A.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线.试说明:
(1)∠MON=
 (∠BON-∠AON);
(∠BON-∠AON);(2)∠MOG=
 (∠AOG+∠BOG).
(∠AOG+∠BOG).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为______.(n≥2,且n为整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1 , 点O2 , 点O3…,则O10的坐标是( )

A.(16+4π,0)
B.(14+4π,2)
C.(14+3π,2)
D.(12+3π,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一组数据:10,17,15,10,18,20,下列说法错误的是( )
A.中位数是16
B.方差是
C.众数是10
D.平均数是15 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接CD.求证:CD⊥BE.
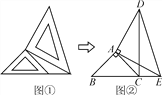
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从教室B到图书馆A,总有少数同学不走人行横道而横穿草坪,他们这种做法是因为________,学校为制止这种现象,准备立一块警示牌,请你为该牌写一句话________________.

相关试题

