【题目】如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1 , 点O2 , 点O3…,则O10的坐标是( )
A.(16+4π,0)
B.(14+4π,2)
C.(14+3π,2)
D.(12+3π,0)
参考答案:
【答案】C
【解析】解:∵点A(2,0),B(0,2),
∴OA=2,OB=2,∠AOB=90°,
∴ ![]() 的长度=
的长度= ![]() =π,
=π,
∵将扇形AOB沿x轴正方向做无滑动的滚动,
∴O1O2= ![]() 的长度=π,
的长度=π,
∴点O1(2,2),点O2(2+π,2),点O3(4+π,0),点O4(6+π,2),…,
∵10÷3=3…1,
∴O10的(14+3π,2).
故选C.
【考点精析】通过灵活运用弧长计算公式,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线.试说明:
(1)∠MON=
 (∠BON-∠AON);
(∠BON-∠AON);(2)∠MOG=
 (∠AOG+∠BOG).
(∠AOG+∠BOG).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为______.(n≥2,且n为整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )

A.
B.3
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一组数据:10,17,15,10,18,20,下列说法错误的是( )
A.中位数是16
B.方差是
C.众数是10
D.平均数是15 -
科目: 来源: 题型:
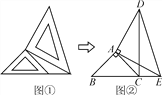
查看答案和解析>>【题目】两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接CD.求证:CD⊥BE.
相关试题

