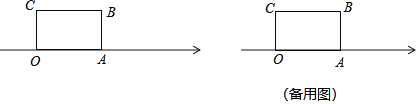
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为几.
(2)将长方形OABC沿OA所在直线水平移动,移动后的长方形记为O′A′B′C′.
①若移动后的长方形O′A′B′C′与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的一半时,求数轴上点A′表示的数.
②若D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,求当长方形OABC移动距离x为何值时,D、E两点到原点O的距离相等?
OO′,求当长方形OABC移动距离x为何值时,D、E两点到原点O的距离相等?
参考答案:
【答案】(1)数轴上点A表示的数为4;(2)①点A′表示的数为2或6;②x=24,或x=![]() .
.
【解析】
(1)利用面积÷OC,可得AO长,进而可得答案;
(2)首先计算出S的值,再根据矩形的面积表示出O′A的长度,再分两种情况:当向左运动时,当向右运动时,分别求出A′表示的数;
(3)此题分两种情况:当原长方形OABC向右移动时,点D,E表示的数都是正数,不符合题意;当原长方形OABC向左移动时,点D表示的数为4-![]() x,点E表示的数为-
x,点E表示的数为-![]() x,再根据题意列出方程.
x,再根据题意列出方程.
(1)∵长方形OABC的面积为12,OC边长为3,
∴OA=12÷3=4,
∴数轴上点A表示的数为4,
故答案为:4.
(2)∵S等于原长方形OABC面积的一半,
∴S=6,
即12-3x=6,
解得x=2.
当向左运动时,如图1,A′表示的数为2;
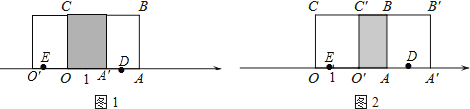
当向右运动时,如图2,
∵O′A′=AO=4,
∴OA′=4+4-2=6,
∴A′表示的数为6;
综上所述,点A′表示的数为2或6;
故答案为:2或6;
(3)当长方形ABCD沿数轴正方向运动时,点D,E表示的数均为正数,不符合题意;
当点D,E所表示的数互为相反数时,长方形ABCD沿数轴负方向运动,画出草图如下:
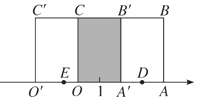
∵点D所表示的数为4-![]() x,点E所表示的数为-
x,点E所表示的数为-![]() x,依题意得
x,依题意得
4-![]() x=-
x=-![]() x,或4-
x,或4-![]() x=
x=![]() x
x
解得x=24,或x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,

(1)按此规律,图案⑦需____根火柴棒;第n个图案需____根火柴棒.
(2)用2018根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3h后安排工人装箱,若每小时装产品150件,未装箱的产品数量(y)是时间(x)的函数,那么这个函数的大致图像只能是( )
A.
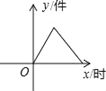 B.
B. 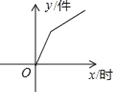 C.
C. 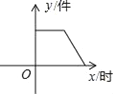 D.
D. 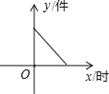
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在同一平面内OA⊥OB,OC是OA绕点O顺时针方向旋转α(α<90°)度得到,OD平分∠BOC,OE平分∠AOC.
(1)若α=60即∠AOC=60°时,求∠BOC,∠DOE.
(2)在α的变化过程中,∠DOE的度数是一个定值吗?若是定值,请求出这个值;若不是定值,请说明理由.

-
科目: 来源: 题型:
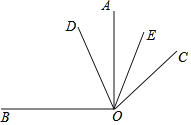
查看答案和解析>>【题目】如图,已知在同一平面内OA⊥OB,OC是OA绕点O顺时针方向旋转α(α<90°)度得到,OD平分∠BOC,OE平分∠AOC.
(1)若α=60即∠AOC=60°时,求∠BOC,∠DOE.
(2)在α的变化过程中,∠DOE的度数是一个定值吗?若是定值,请求出这个值;若不是定值,请说明理由.
-
科目: 来源: 题型:
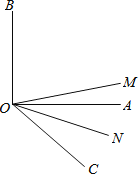
查看答案和解析>>【题目】已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°
(1)若∠AOC=40°,求∠AOM和∠MON的大小;
(2)当锐角∠AOC的度数发生改变时,∠MON的大小是否发生改变?如不会改变,请写出∠MON的大小,并写出推理过程;如会改变,也请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
相关试题

