【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,

(1)按此规律,图案⑦需____根火柴棒;第n个图案需____根火柴棒.
(2)用2018根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
参考答案:
【答案】(1)图案⑦需50根火柴棒;图案n需火柴棒7n+1根;(2)2017是第288个图案.理由见解析.
【解析】
(1)根据图案①、②、③中火柴棒的数量可知,第1个图形中火柴棒有8根,每多一个多边形就多7根火柴棒,由此可知第n个图案需火柴棒8+7(n-1)=7n+1根,令n=7可得答案.
(2)令8+7(n-1)=7n+1=2017求得n值即可.
解:(1)∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
∴图案n需火柴棒:8+7(n-1)=7n+1根;
当n=7时,7n+1=7×7+1=50,
∴图案⑦需50根火柴棒;
(2)令7n+1=2017,
解得n=288,
故2017是第288个图案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价15%后的售价为1.15元,则该商品在甲商场的原价为 ▲ 元;
(2)乙商场将该商品提价20%后,用6元钱购买该商品的件数比没提价前少买1件,求该商品在乙商场的原价是多少?
(3)在(1)、(2)小题的条件下,甲、乙两商场把该商品均按原价进行了两次价格调整.
甲商场:第一次提价的百分率是
 ,第二次提价的百分率是
,第二次提价的百分率是 ;
;乙商场:两次提价的百分率都是
 (
( .
.请问甲、乙两商场,哪个商场的提价较多?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三张正面分别写有数字-1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
A.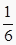
B.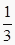
C.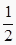
D.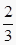
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3h后安排工人装箱,若每小时装产品150件,未装箱的产品数量(y)是时间(x)的函数,那么这个函数的大致图像只能是( )
A.
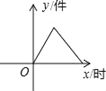 B.
B. 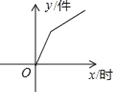 C.
C. 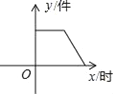 D.
D. 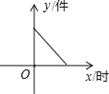
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在同一平面内OA⊥OB,OC是OA绕点O顺时针方向旋转α(α<90°)度得到,OD平分∠BOC,OE平分∠AOC.
(1)若α=60即∠AOC=60°时,求∠BOC,∠DOE.
(2)在α的变化过程中,∠DOE的度数是一个定值吗?若是定值,请求出这个值;若不是定值,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为几.
(2)将长方形OABC沿OA所在直线水平移动,移动后的长方形记为O′A′B′C′.
①若移动后的长方形O′A′B′C′与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的一半时,求数轴上点A′表示的数.
②若D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,求当长方形OABC移动距离x为何值时,D、E两点到原点O的距离相等?
OO′,求当长方形OABC移动距离x为何值时,D、E两点到原点O的距离相等?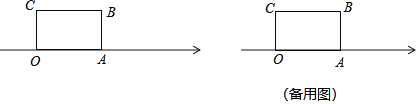
相关试题

