搜索
【题目】某校师生到离校 
千米远的实习基地培训，甲组师生骑自行车，乙组师生步行，已知骑自行车的速度是步行速度的 
倍. 若甲，乙两组同时出发，结果乙组师生比甲组迟 
小时到达目的地，那么乙组师生每小时步行多少千米？
参考答案：
【答案】解：设乙组师生的步行速度为 
/小时，则骑车速度是 
/小时 
解得 
经检验， 是该方程的解
答：乙组师生每小时步行5千米.
【解析】设乙组师生的步行速度为 x k m /小时，则骑车速度是 3 x k m /小时 ，等量关系是：乙组师生比甲组迟 2 小时到达目的地，可列方程求解.
【考点精析】根据题目的已知条件，利用分式方程的应用的相关知识可以得到问题的答案，需要掌握列分式方程解应用题的步骤：审题、设未知数、找相等关系列方程、解方程并验根、写出答案（要有单位）．
-
科目： 来源： 题型：
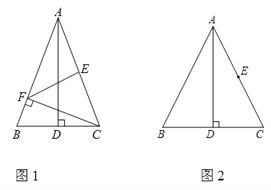
查看答案和解析>>【题目】在锐角△ABC中，AB=AC，AD为BC边上的高，E为AC中点．
（1）如图1，过点C作CF⊥AB于F点，连接EF．若∠BAD=20°，求∠AFE的度数；
（2）若M为线段BD上的动点（点M与点D不重合），过点C作CN⊥AM于N点，射线EN，AB交于P点．
①依题意将图2补全；
②小宇通过观察、实验，提出猜想：在点M运动的过程中，始终有∠APE=2∠MAD．
小宇把这个猜想与同学们进行讨论，形成了证明该猜想的几种想法：
想法1：连接DE，要证∠APE=2∠MAD，只需证∠PED=2∠MAD．
想法2：设∠MAD=α，∠DAC=β，只需用α，β表示出∠PEC，通过角度计算得∠APE=2α．
想法3：在NE上取点Q，使∠NAQ=2∠MAD，要证∠APE=2∠MAD，只需证△NAQ∽△APQ．……
请你参考上面的想法，帮助小宇证明∠APE =2∠MAD．（一种方法即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】司机小王沿东西大街跑出租车，约定向东为正，向西为负，某天自A地出发到收工时，行走记录为（单位：千米）：+8、﹣9、+7、﹣2、+5、﹣10、+7、﹣3，回答下列问题：
（1）记录中“+8”表示什么意思？
（2）收工时小王在A地的哪边？距A地多少千米？
（3）若每千米耗油0.2升，问从A地出发到收工时，共耗油多少升？
-
科目： 来源： 题型：
查看答案和解析>>【题目】按要求解答：
（1）计算：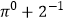
；
（2）因式分解：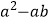
；
（3）先化简，再求值：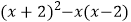
，其中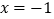 
. -
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解某校初三年级400名学生的体重情况，从中抽查了50名学生的体重进行统计分析，在这个问题中，总体是（ ）
A.400名学生的体重
B.被抽取的50名学生
C.400名学生
D.被抽取的50名学生的体重 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，BC为弦，D为
的中点，AC，BD相交于E点，过点A作⊙O的切线交BD的延长线于P点．
（1）求证：∠PAC=2∠CBE；
（2）若PD=m，∠CBE=α，请写出求线段CE长的思路．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了让市民享受到更多的优惠，某市针对乘坐地铁的人群进行了调查．
（1）为获得乘坐地铁人群的月均花费信息，下列调查方式中比较合理的是 ；
A．对某小区的住户进行问卷调查
B．对某班的全体同学进行问卷调查
C．在市里的不同地铁站，对进出地铁的人进行问卷调查
（2）调查小组随机调查了该市1000人上一年乘坐地铁的月均花费（单位：元），绘制了频数分布直方图，如图所示．
① 根据图中信息，估计平均每人乘坐地铁的月均花费的范围是 元；
A．20—60 B．60—120 C．120—180
②为了让市民享受到更多的优惠，相关部门拟确定一个折扣线，计划使30%左右的人获得折扣优惠．根据图中信息，乘坐地铁的月均花费达到 元的人可以享受折扣．
相关试题
