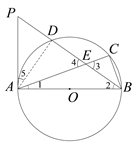
【题目】如图,AB是⊙O的直径,BC为弦,D为![]() 的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.

(1)求证:∠PAC=2∠CBE;
(2)若PD=m,∠CBE=α,请写出求线段CE长的思路.
参考答案:
【答案】(1)证明见解析; (2)思路见解析.
【解析】(1)证明:∵D为![]() 的中点
的中点
,
∴∠CBA=2∠CBE.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠1+∠CBA=90°.
∴∠1+2∠CBE =90°.
∵AP是⊙O的切线,
∴∠PAB=∠1+∠PAC=90°.
∴∠PAC =2∠CBE.
(2)思路:①连接AD,由D是![]() 的中点,∠2=∠CBE,
的中点,∠2=∠CBE,
由∠ACB=∠PAB=90°,得∠P=∠3=∠4,故AP=AE;
②由AB是⊙O的直径,可得∠ADB=90°;由AP=AE,
得PE=2PD=2m,∠5=![]() ∠PAC =∠CBE=
∠PAC =∠CBE= ![]()
③在Rt△PAD中,由PD=m,∠5= ![]() ,可求PA的长;
,可求PA的长;
④在Rt△PAB中,由PA的长和∠2= ![]() ,可求BP的长;
,可求BP的长;
由![]() 可求BE的长;
可求BE的长;
⑤在Rt△BCE中,由BE的长和![]() ,可求CE的长.
,可求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解答:
(1)计算: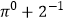 ;
;
(2)因式分解: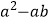 ;
;
(3)先化简,再求值: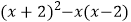 ,其中
,其中 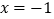 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校师生到离校
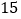 千米远的实习基地培训,甲组师生骑自行车,乙组师生步行,已知骑自行车的速度是步行速度的
千米远的实习基地培训,甲组师生骑自行车,乙组师生步行,已知骑自行车的速度是步行速度的 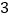 倍. 若甲,乙两组同时出发,结果乙组师生比甲组迟
倍. 若甲,乙两组同时出发,结果乙组师生比甲组迟 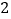 小时到达目的地,那么乙组师生每小时步行多少千米?
小时到达目的地,那么乙组师生每小时步行多少千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校初三年级400名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是( )
A.400名学生的体重
B.被抽取的50名学生
C.400名学生
D.被抽取的50名学生的体重 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让市民享受到更多的优惠,某市针对乘坐地铁的人群进行了调查.
(1)为获得乘坐地铁人群的月均花费信息,下列调查方式中比较合理的是 ;
A.对某小区的住户进行问卷调查
B.对某班的全体同学进行问卷调查
C.在市里的不同地铁站,对进出地铁的人进行问卷调查
(2)调查小组随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.

① 根据图中信息,估计平均每人乘坐地铁的月均花费的范围是 元;
A.20—60 B.60—120 C.120—180
②为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.根据图中信息,乘坐地铁的月均花费达到 元的人可以享受折扣.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=﹣1,xy=3,则x2y+xy2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a+2a2=3a2 B. x3﹣4x3=﹣3x3 C. 2xy2+3x2y=5x2y2 D. ﹣x2﹣2x2=3x2
相关试题

