【题目】如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为![]() =2cm/s,
=2cm/s,![]() =1cm/s,当点P到达点B时,P,Q两点同时停止运动,设点P的运动时间为t秒.
=1cm/s,当点P到达点B时,P,Q两点同时停止运动,设点P的运动时间为t秒.

(1)用含t的代数式表示BP=______,BQ=_______;
(2)当t为何值时,△BPQ为等边三角形?
(3)当t为何值时,△BPQ为直角三角形?
参考答案:
【答案】(1)6-2t,t.(2)当t=2s时△PBQ为等边三角形;(3)当t为1.5s或2.4s时△PBQ为直角三角形.
【解析】
(1)由题意可知AP=2t,BQ=t.再根据线段的和差关系即可求解;
(2)当△PBQ为等边三角形时,则有BP=BQ,即6-2t=t,可求得t;
(3)当PQ⊥BQ时,在Rt△PBQ中,BP=2BQ,可得6-2t=2t;当PQ⊥BP时,可得BQ=2BP,可得2t=2(6-2t)分别求得t的值即可.
解:(1)依题意,得:AP=2t,BQ=t.
∵AB=6,
∴BP=AB-AP=6-2t.
故答案为6-2t,t.
由(1)可知AP=2t,BQ=t,则BP=AB-AP=6-2t,
∵△PBQ为等边三角形,
∴BP=BQ,
即6-2t=t,
解得t=2,
∴当t=2s时△PBQ为等边三角形;
(3)①当PQ⊥BQ时,
∵∠B=60°,
∴∠BPQ=30°,
∴在Rt△PBQ中,BP=2BQ,
即6-2t=2t,
解得t=1.5;
②当PQ⊥BP时,同理可得BQ=2BP,即t=2(6-2t),解得t=2.4,
综上可知当t为1.5s或2.4s时△PBQ为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在用描点法画二次函数
 的图象时,列出下面的表格:
的图象时,列出下面的表格:
…





…

…





…
根据表格提供的信息,下列说法错误的是( )
A. 该抛物线的对称轴是直线
 B. 该抛物线与
B. 该抛物线与 轴的交点坐标为
轴的交点坐标为C.
 D. 若点
D. 若点 是该抛物线上一点.则
是该抛物线上一点.则
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,垂足为E,若DE=2cm,则BD的长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标为(-3,4),作出点P关于x轴对称的点P1,称为第1次变换;再作出点P1关于y轴对称的点P2,称为第2次变换;再作点P2关于x轴对称的点P3,称为第3次变换,…,依次类推,则第2019次变换得到的点P2019的坐标为 ____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
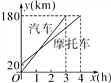
A. 2个 B. 3个 C. 4个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )

A.4B.5C.
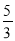 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① ;②
;② ;③
;③ ;④
;④ .其中正确的结论是( )
.其中正确的结论是( )
A. ①② B. ②③ C. ③④ D. ②④
相关试题

