【题目】如图1,抛物线 y=ax2+bx+c 与 x 轴交于A(1,0),B(-3,0),与 y 轴交于C(0,3),顶点是G.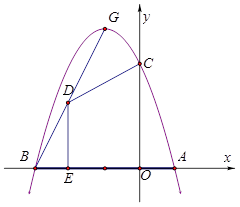
(1)求抛物线的的解析式及顶点坐标G.
(2)如图1,点D(x,y)是线段BG上的动点(不与B,G重合),DE⊥x轴于E,设四边形OEDC的面积为S,求S与x之间的函数关系式,并求S的最大值.
(3)如图2,将抛物线 y=ax2+bx+c 向下平移 k 个单位,平移后的顶点式 G' ,与 x 轴的交点是 A',B' .若△A'B'G' 是直角三角形,求 k 的值.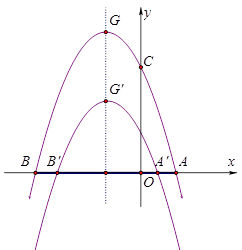
参考答案:
【答案】
(1)解:∵与 x 轴的交点为A(1,0),B(-3,0),
∴设二次函数为 y=a(x+1)(x3),
把C(0,3)代入 y=a(x+1)(x3),
∴ a=-1 ,
∴ y=-x2-2x+3=-(x+1)2+4.
∴G(-1,4).
(2)解:设直线BG解析式为 :y=kx+b
∵B(3,0),G(1,4) 在直线BG上,
∴![]() ,
,
∴![]() ,
,
∴ 直线BG解析式为:y=2x+6,
∴ D(x,2x+6)
∴ S=![]() =
=![]() =-x2-
=-x2-![]() x ( 3<x<1 ),
x ( 3<x<1 ),
当 x=-![]() =-
=-![]() 时,Smax=
时,Smax=![]() .
.
(3)解:设平移后的抛物线为 y=(x+1)2+m,
∴G'(-1,m),A'(-1-![]() ,0),B'(-1+
,0),B'(-1+![]() ,0),
,0),
∴A'B'=2![]() ,B'G'=A'G'=
,B'G'=A'G'=![]() ,
,
∵△A'B'G'为直角三角形,
∴B'G'2+A'G'2=A'B'2,
∴m2m=0,
∴ m1=1 , m2=0 (舍),
∴ y=(x+1)2+1,
∵由 y=(x+1)2+4 得到 y=(x+1)2+1
∴ 向下平移3个单位,
∴ k=3.
【解析】(1)根据题意可设二次函数为 y=a(x+1)(x3),将C(0,3)代入 y=a(x+1)(x3),从而求出抛物线解析式,即可得出顶点坐标.
(2)设直线BG解析式为 :y=kx+b把B(3,0),G(1,4) 代入即可得到一个二元一次方程组,解之即可得出直线BG解析式为:y=2x+6,从而表示D(x,2x+6),再由S=![]() =
=![]() =-x2-
=-x2-![]() x ( 3<x<1 ),由二次函数的性质得出当 x=-
x ( 3<x<1 ),由二次函数的性质得出当 x=-![]() =-
=-![]() 时,Smax=
时,Smax=![]() .
.
(3)设平移后的抛物线为 y=(x+1)2+m,根据题意得G'(-1,m),A'(-1-![]() ,0),B'(-1+
,0),B'(-1+![]() ,0),A'B'=2
,0),A'B'=2![]() ,B'G'=A'G'=
,B'G'=A'G'=![]() ,
,
在Rt△A'B'G'中,由勾股定理得m2m=0,从而求出m值,即可得出k值.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握二次函数图象的平移(平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,C是圆周上的动点,P是优弧中点.

(1)求证:OP∥BC.
(2)连接PC交直径AB于点D,当OC=DC时,求∠A的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个完全相同的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为___________s

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:22﹣21=2×21﹣1×21=2( )
23﹣22= =2( ),
24﹣23= =2( ),
……
(1)请仔细观察,写出第4个等式;
(2)请你找规律,写出第n个等式;
(3)计算:21+22+23+…+22019﹣22020.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(﹣1)23×(π﹣3)0﹣(﹣
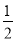 ) ﹣3;
) ﹣3;(2)aa2a3+(﹣2a3)2﹣a8÷a2;
(3)(x+4)2﹣(x+2)(x﹣2);
(4)(a+2b﹣3c)(a﹣2b+3c).
相关试题

