【题目】已知AB是⊙O的直径,C是圆周上的动点,P是优弧中点.
(1)求证:OP∥BC.
(2)连接PC交直径AB于点D,当OC=DC时,求∠A的度数.
参考答案:
【答案】
(1)证明:连接AC,延长PO交AC于H,如图1,

∵P是优弧的中点,
∴PH⊥AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC⊥AC,
∴OP∥BC.
(2)解:连接AC,延长PO交AC于H,如图2,

∵P是优弧的中点,
∴PA=PC,
∴∠PAC=∠PCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠PAO=PCO,
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x,
∴∠PDO=2x,
∴∠ODC=∠POD+∠OPC=3x,
∵CD=CO,
∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
∴x=![]() ,
,
即∠PAO=![]() ,
,
∴∠A的度数为![]()
![]()
【解析】(1)连接AC,延长PO交AC于H,由垂径定理推论得PH⊥AC,再由圆周角定理得BC⊥AC,根据垂直于同一条直线的两条直线平行即可得证.
(2)连接AC,延长PO交AC于H,如图2,由垂径定理推论得PA=PC, 根据等腰三角形的性质得∠PAC=∠PCA,∠OAC=∠OCA,等量代换得
∠PAO=PCO;当CO=CD时,设∠DCO=x,则∠OPC=x,∠PAO=x,由三角形的外角和性质得 ∠ODC=3x,在△POC中,再根据三角形的内角和定理得出
x+x+5x=180°,从而求出∠A的度数![]() .
.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△ABC的面积为8cm2,则△CEF的面积为( )

A.0.5cm2B.1cm2C.2cm2D.4cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在湖州创建国家卫生文明城市的过程中,张辉和夏明积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:①清理类岗位:清理花坛卫生死角;清理楼道杂物(分别用
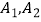 表示)。
表示)。
②宣传类岗位:垃圾分类知识宣传;交通安全知识宣传(分别用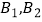 表示)。
表示)。
(1)张辉同学从四个岗位中随机选取一个报名,恰好选择清理类岗位概率为是;
(2)若张辉和夏明各随机从四个岗位中选一个报名,请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个完全相同的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为___________s

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:22﹣21=2×21﹣1×21=2( )
23﹣22= =2( ),
24﹣23= =2( ),
……
(1)请仔细观察,写出第4个等式;
(2)请你找规律,写出第n个等式;
(3)计算:21+22+23+…+22019﹣22020.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线 y=ax2+bx+c 与 x 轴交于A(1,0),B(-3,0),与 y 轴交于C(0,3),顶点是G.
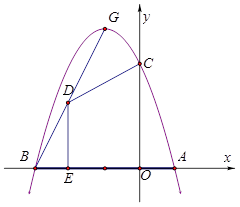
(1)求抛物线的的解析式及顶点坐标G.
(2)如图1,点D(x,y)是线段BG上的动点(不与B,G重合),DE⊥x轴于E,设四边形OEDC的面积为S,求S与x之间的函数关系式,并求S的最大值.
(3)如图2,将抛物线 y=ax2+bx+c 向下平移 k 个单位,平移后的顶点式 G' ,与 x 轴的交点是 A',B' .若△A'B'G' 是直角三角形,求 k 的值.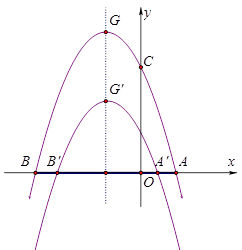
相关试题

