【题目】某市为解决农村燃气困难,在P处建立了一个燃气站,从P站分别向A、B、C村铺设燃气管道。已知B村在A村的北偏东60°方向,距离A村2.4km,C村在A村的正东方向,距离A村1.8km,要使此工程费用最省,管道PA+PB+PC之和需最短,则最短长度为______________km.

参考答案:
【答案】3
【解析】
先证明△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.然后根据这个原理找到点P,把△APC绕点A逆时针旋转60°得△ADE,证得△ABE是直角三角形,用勾股定理求出BE,即可得出PA+PB+PC之和的最短值。
解:先证明结论:△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
如图1, P为△ABC内一点,∠APB=∠BPC=120°,
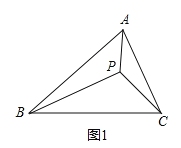
证明:如图2,将△ACP绕点A逆时针旋转60°得到△ADE,

∴∠PAD=60°,△PAC≌△DAE,
∴PA=DA、PC=DE、∠APC=∠ADE=120°,
∴△APD为等边三角形,
∴PA=PD,∠APD=∠ADP=60°,
∴∠APB+∠APD=120°+60°=180°,∠ADP+∠ADE=180°,即B、P、D、E四点共线,
∴PA+PB+PC=PD+PB+DE=BE.
∴PA+PB+PC的值最小.
解决问题:
如图3,将三个村连接为△ABC,由上可知,当∠APB=∠APC=∠BPC=120°时,AP+BP+PC的值最小.
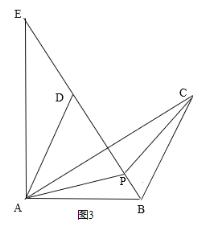
把△APC绕点A逆时针旋转60°得△ADE,
∴∠PAD=60°,AE=AC=2.4 km
由上可知B、P、D、E共线,且AP+BP+PC=BE,∠PAB=∠DAE,
∵B村在A村的北偏东60°方向, C村在A村的正东方向,
∴∠BAC=30°,
∴∠PAB+∠PAC=∠DAE+∠PAB=30°,
∴∠BAE=∠DAE+∠PAB+∠PAD=90°,
在Rt△ABE中,
![]()
∴PA+PB+PC=3km
故答案为:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)写出点
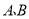 的坐标
的坐标(2)线段
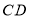 先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段
先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段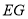 重合.
重合.(3)已知在
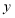 轴上存在点
轴上存在点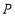 与
与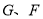 围成的三角形面积为6,请写出
围成的三角形面积为6,请写出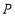 的坐标
的坐标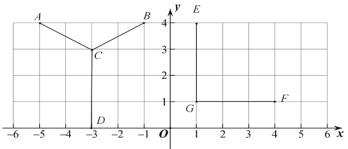
-
科目: 来源: 题型:
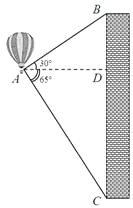
查看答案和解析>>【题目】(6分)如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在双曲线y=
 上,点B在双曲线y=
上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
A. 6 B. 9 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,依次有3个三角形放置在上面,它们分别是等边三角形、等腰直角三角形、含30°角的直角三角形,直接填写出∠1、∠2、∠3 的度数.

∠1= °;∠2= °;∠3= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是8×8的标准点阵图,直线l、m互相垂直,已知△ABC.

(1)写出△ABC的形状;
(2)分别画出△ABC关于直线l、m对称的△A1B1C1,△A2B2C2,再画出△A1B1C1关于直线m对称的△A3B3C3
(3)△A2B2C2与△A3B3C3关于哪条直线对称? (填“直线l、m”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年6月22日至7月2日,11天湖南地区持续降大到暴雨,总量达570亿立方米的雨水从天而降,倾泻到三湘大地,全省14个市州120个县(市、区)1621个多镇受灾,现有三批救灾物资从长沙岀发送往某受灾乡镇,前两批物资运货情况如图所示:
火车皮(单位:节)
汽车(单位:辆)
物质重量(单位:吨)
第一批
4
16
264
第二批
6
10
340
(1)每节火车皮和每辆汽车平均各能装多少吨物资?
(2)已知火车皮的装运费为30元吨,汽车的装运费为100元/吨.若第三批救灾物资需要5节火车皮和15辆汽车正好装完,共需要装运费多少元?
相关试题

