【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.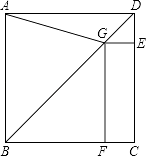
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
参考答案:
【答案】
(1)
解:结论:AG2=GE2+GF2.
理由:连接CG.
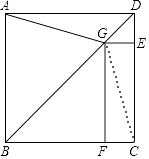
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2
(2)
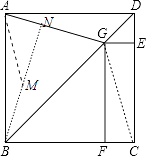
解:作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,MN= ![]() x,
x,
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x2+(2x+ ![]() x)2,
x)2,
解得x= ![]() ,
,
∴BN= ![]() ,
,
∴BG=BN÷cos30°= ![]() .
.
【解析】(1)结论:AG2=GE2+GF2 . 只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN= ![]() x,在Rt△ABN中,根据AB2=AN2+BN2 , 可得1=x2+(2x+
x,在Rt△ABN中,根据AB2=AN2+BN2 , 可得1=x2+(2x+ ![]() x)2 , 解得x=
x)2 , 解得x= ![]() ,推出BN=
,推出BN= ![]() ,再根据BG=BN÷cos30°即可解决问题;
,再根据BG=BN÷cos30°即可解决问题;
【考点精析】掌握勾股定理的概念和正方形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.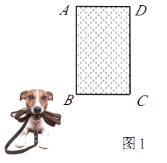
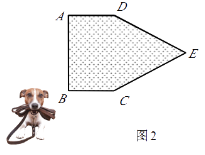
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
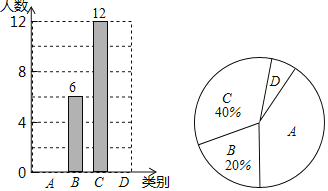
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
-
科目: 来源: 题型:
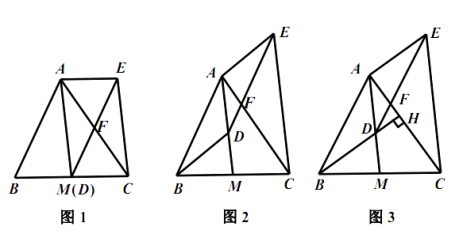
查看答案和解析>>【题目】△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=_____度;

(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=_______度;

(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________.
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
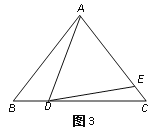
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
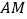 是
是 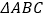 的中线,
的中线, 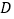 是线段
是线段 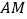 上一点(不与点
上一点(不与点 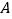 重合).
重合). 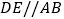 交
交 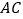 于点
于点 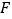 ,
, 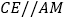 ,连结
,连结 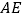 .
.
(1)如图1,当点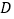 与
与 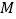 重合时,求证:四边形
重合时,求证:四边形 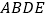 是平行四边形;
是平行四边形;
(2)如图2,当点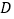 不与
不与 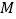 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长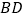 交
交 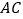 于点
于点 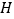 ,若
,若 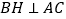 ,且
,且 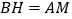 .当
.当 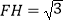 ,
, 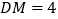 时,求
时,求 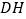 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )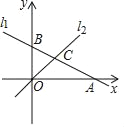
A.
 B.
B.  C.
C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.

(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
相关试题

