搜索
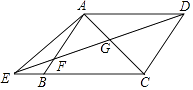
【题目】如图，已知在四边形ABCD中，AD∥BC，E为边CB延长线上一点，联结DE交边AB于点F，联结AC交DE于点G，且 
= 
． 
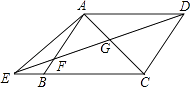
（1）求证：AB∥CD；
（2）如果AD2=DGDE，求证： 
= 
．
参考答案：
【答案】
（1）证明：∵AD∥BC，
∴△ADG∽△CEG，
∴ 
，
∵ 
= 
，
∴ 
，
∴AB∥CD
（2）证明：∵AD∥BC，
∴△ADG∽△CEG，
∴ 
，
∴ 
= 
，
∴ 
= 
，
∵AD2=DGDE，
∴ = 
，
∵AD∥BC，
∴ 
= ，
∴ = ．
【解析】（1）由AD∥BC，得到△ADG∽△CEG，根据相似三角形的性质即可得到结论；（2）根据平行线的性质得到 ，根据等式的性质得到 = ，等量代换即可得到结论．
-
科目： 来源： 题型：
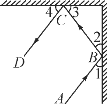
查看答案和解析>>【题目】如图，一束光线在两面玻璃墙内进行传播，路径为A→B→C→D，根据光的反射性质，∠1＝∠2，∠3＝∠4，若∠2＋∠3＝90°，试探究直线AB与CD是否平行？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人都去同一家超市购买大米各两次，甲每次购买50千克的大米，乙每次购买50元的大米，这两人第一次购买大米时售价为每千克m元，第二次购买大米时售价为每千克n元(m≠n)，若规定谁两次购买大米的平均单价低，谁的购买方式就合算，则下列观点正确的是( )
A. 甲的购买方式合算 B. 乙的购买方式合算
C. 甲、乙的购买方式同样合算 D. 不能判断谁的购买方式合算
-
科目： 来源： 题型：
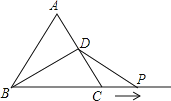
查看答案和解析>>【题目】如图，等边△ABC的边长为10cm，点D是边AC的中点，动点P从点C出发，沿BC的延长线以2cm/s的速度做匀速运动，设点P的运动时间为t（秒），若△BDP是等腰三角形，求t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）某工厂计划在规定时间内生产24000个零件，若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．
（1）求原计划每天生产的零件个数和规定的天数．
（2）为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%，按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面的材料，然后解答问题．
通过计算，发现：
方程x＋
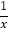＝2＋
的解为x＝2或x＝；方程x＋
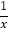＝3＋
的解为x＝3或x＝；方程x＋
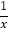＝4＋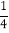
的解为x＝4或x＝；…
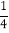(1)观察猜想：求关于x的方程x＋
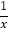＝n＋
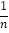的解；(2)实践运用：对于关于x的方程x－
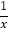＝m－
的解，小明观察得“x＝m”是该方程的一个解，请你猜想该方程的另一个解，并用方程的解的概念对该解进行验证；(3)拓展延伸：请利用上面的规律，求关于x的方程x＋
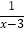＝a＋
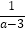的解． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在平面直角坐标系xOy中，二次函数y=﹣x2+mx+n的图象经过点A（3，0），B（m，m+1），且与y轴相交于点C．
（1）求这个二次函数的解析式并写出其图象顶点D的坐标；
（2）求∠CAD的正弦值；
（3）设点P在线段DC的延长线上，且∠PAO=∠CAD，求点P的坐标．
相关试题
