【题目】我们在小学已经学过了“对边分别平行的四边形叫做平行四边形”,如图1,平行四边形MNPQ的一边PQ作左右平移,图2反映它的边NP的长度(cm)随时间t(s)变化而变化的情况,请解答下列问题:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)观察图2,PQ向左平移前,边NP的长度是______cm,请你根据图象呈现的规律写出0至5秒间l与t的关系式;
(3)填写下表,并根据表中呈现的规律写出8至14秒间1与t的关系式.
PQ边的运动时间/s | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
NP的长度/cm | 18 | 15 | 12 | ______ | 6 | 3 | 0 |

参考答案:
【答案】(1)t,NP(2)(2t+8)(3)9
【解析】
(1)根据自变量和因变量的概念即可得出结论;
(2)利用待定系数法即可得出结论;
(3)利用待定系数法即可得出结论.
(1)这个变化过程中,自变量是时间t、因变量NP的长度,
故答案为:t,NP;
(2)由图2知,0至5秒间图象呈现的是一段线段,且过点(0,8),(5,18),
设此线段的解析式为NP=kt+8(0≤t≤5),
∴18=5k+8,
∴k=2,
∴线段的解析式为NP=2t+8(0≤t≤5),
故答案为(2t+8);
(3)由图2知,8至14秒间图象呈现的也是一段线段,
由表知,此线段过点(8,18),(14,0),
设此线段的解析式为NP=k't+b(8≤t≤14),
∴![]() ,
,
∴![]() ,
,
∴NP=-3t+42(8≤t≤14),
当t=11时,NP=-3×11+42=9,
故答案为9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与
 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:① 4ac<b2;② 方程ax2+bx+c=0的两个根是
 ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;其中结论正确有__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司技术人员用“沿直线AB折叠检验塑胶带两条边缘线a、b是否互相平行”.
(1)如图1,测得∠1=∠2,可判定a∥b吗?请说明理由;
(2)如图2,测得∠1=∠2,且∠3=∠4,可判定a∥b吗?请说明理由;
(3)如图3,若要使a∥b,则∠1与∠2应该满足什么关系式?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由7块颜色不同的正方形组成的长方形,已知中间小正方形的边长为1,这个长方形的面积为( )

A.45B.48C.63D.64
-
科目: 来源: 题型:
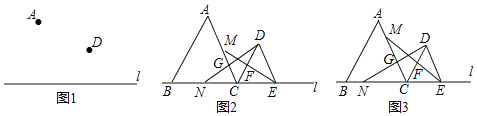
查看答案和解析>>【题目】已知点A、D在直线l的同侧.
(1)如图1,在直线l上找一点C.使得线段AC+DC最小(请通过画图指出点C的位置);
(2)如图2,在直线l上取两点B、E,恰好能使△ABC和△DCE均为等边三角形.M、N分别是线段AC、BC上的动点,连结DN交AC于点G,连结EM交CD于点F.
①当点M、N分别是AC、BC的中点时,判断线段EM与DN的数量关系,并说明理由;
②如图3,若点M、N分别从点A和B开始沿AC和BC以相同的速度向点C匀速运动,当M、N与点C重合时运动停止,判断在运动过程中线段GF与直线1的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=
 ,AE=3,求AF的长.
,AE=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
相关试题

