【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )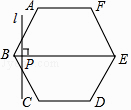
A.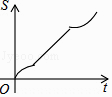
B.
C.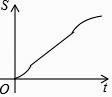
D.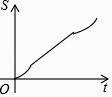
参考答案:
【答案】C
【解析】解:由题意得:BP=t,
如图1,连接AC,交BE于G,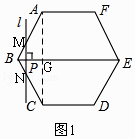
Rt△ABG中,AB=6,∠ABG=60°,
∴∠BAG=30°,
∴BG= ![]() AB=3,
AB=3,
由勾股定理得:AG= ![]() =3
=3 ![]() ,
,
∴AC=2AG=6 ![]() ,
,
当0≤t≤3时,PM= ![]() t,
t,
∴MN=2 ![]() t,
t,
S=S△BMN= ![]() MNPB=
MNPB= ![]() =
= ![]() ,
,
所以选项A和B不正确;
如图2,当9≤t≤12时,PE=12﹣t,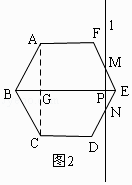
∵∠MEP=60°,
∴tan∠MEP= ![]() ,
,
∴PM= ![]() (12﹣t),
(12﹣t),
∴MN=2PM=2 ![]() (12﹣t),
(12﹣t),
∴S=S正六边形﹣S△EMN ,
=2× ![]() (AF+BE)×AG﹣
(AF+BE)×AG﹣ ![]() MNPE,
MNPE,
=(6+12)×3 ![]() ﹣
﹣ ![]() ×
× ![]() (12﹣t)(12﹣t),
(12﹣t)(12﹣t),
=54 ![]() ﹣
﹣ ![]() (144﹣24t+t2),
(144﹣24t+t2),
=﹣ ![]() +24
+24 ![]() t﹣90
t﹣90 ![]() ,
,
此二次函数的开口向下,
所以选项C正确,选项D不正确;
故选C.
从给出的图象中看,中间位置的图象一致,只要计算两边取值中的图象即可作出判断;先计算点P从B到G时扫过的面积S,发现是二次函数,且开口向下,可以否定和B,再计算点P从9≤t≤12时扫过的面积为正六边形的面积﹣△EMN的面积,计算得到一个开口向下的二次函数,由此作判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班准备购买大课间活动器材呼啦圈和跳绳,已知购买1根跳绳和2个呼啦圈要35元,购买2根跳绳和1个呼啦圈要25元.
(1)求每根跳绳、每个呼啦圈各多少元?
(2)根据班级实际情况,需购买跳绳和呼啦圈的总数量为30,总费用不超过300元,但不低于280元,请你通过计算求出有几种购买方案,哪种方案费用最低. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=8,C是线段MN上一动点,在MN的同侧分别作等边△CMD和等边△CNE.
(1)如图①,连接DN与EM,两条线段相交于点H,求证ME=DN,并求∠DHM的度数;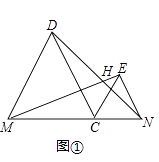
(2)如图②,过点D、E分别作线段MN的垂线,垂足分别为F、G,问:在点C运动过程中,DF+EG的长度是否为定值,如果是,请求出这个定值,如果不是请说明理由;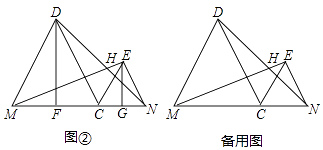
(3)当点C由点M移到点N时,点H移到的路径长度为(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x﹣2与x轴交于点A,与y轴交于点C,经过A、C两点的抛物线与轴交于另一点B(1,0).
x﹣2与x轴交于点A,与y轴交于点C,经过A、C两点的抛物线与轴交于另一点B(1,0).
(1)求该抛物线的解析式.
(2)在直线y= x﹣2上方的抛物线上存在一动点D,连接AD、CD,设点D的横坐标为m,△DCA的面积为S,求S与m的函数关系式,并求出S的最大值.
x﹣2上方的抛物线上存在一动点D,连接AD、CD,设点D的横坐标为m,△DCA的面积为S,求S与m的函数关系式,并求出S的最大值.
(3)在抛物线上是否存在一点M,使得以M为圆心,以 为半径的圆与直线AC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
为半径的圆与直线AC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
(4)在y轴的正半轴上存在一点P,使∠APB的值最大,请直接写出当∠APB最大时点P的坐标. -
科目: 来源: 题型:
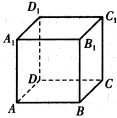
查看答案和解析>>【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)解不等式组 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来. 
(2)解方程 =1﹣
=1﹣  .
.
相关试题

