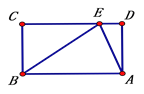
【题目】如图,矩形ABCD中,AB=10,BC=6,点E为CD边上一点。
(1)当AE平分∠BED时,求DE的长。
(2)你能把矩形ABCD沿某条直线剪一刀分成两块,再拼成一个菱形吗?如果能,在备用图中画出示意图,并计算菱形较长对角线的长。

参考答案:
【答案】(1)2;(2)作图见解析.
【解析】整体分析:
(1)过点A作AF⊥BE,用面积法得BE=AB,在Rt△BCE中,用勾股定理求CE的长,即可求DE;(2)根据四边相等的四边形是菱形,沿BE剪一刀后,将△BCE向右边平移6个单位,构造直角三角形,用勾股定理求较长对角线的长.
解:(1)如图,过点A作AF⊥BE,
∵AE平分∠BED,AD⊥DE,AF⊥EF,
∴AD=AF,
∵2S△EAB=AB×AD=BE×AF,
∴AB=BE,
∵AB=10,∴BE=10,
Rt△BCE中,BC=6,由勾股定理得CE=8.
∴DE=CD-CE=10-8=2.
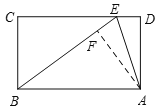
(2)如图,在矩形ABCD中,在CD边上取点E,使CE=8,则DE=2,
沿BE剪一切,则BE=10,再将△BCE向右平移6个单位长度,使BC与AD重合,所得四边形ABEC′即为菱形.
BC′=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,
 ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为
),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为  .
.
(1)求a的值;
(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;
(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
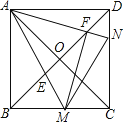
(1)求证: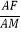 =
= 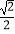 ;
;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明. -
科目: 来源: 题型:
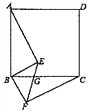
查看答案和解析>>【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=6cm,BC=4 cm,E为CD中点.点P从A点出发,沿A—B—C的方向在矩形边上匀速运动,速度为1 cm /s,运动到C点停止.设点P运动的时间为t s.(图2为备用图)
(1)当P在AB上,t为何值时,△APE的面积是矩形ABCD面积的
 ?
?(2)在整个运动过程中,t为何值时,△APE为等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab

D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的
座位数
第2排的
座位数
第3排的
座位数
第4排的
座位数
…
a
a+2
a+4
…
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
相关试题

