【题目】如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.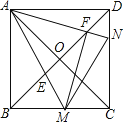
(1)求证: ![]() =
= ![]() ;
;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,∠ABC=90°,
∵∠MAN=45°,
∴∠MAF=∠MBE,
∴A、B、M、F四点共圆,
∴∠ABM+∠AFM=180°,
∴∠AFM=90°,
∴∠FAM=∠FMA=45°,
∴AM= ![]() AF,
AF,
![]()
![]()
(2)
证明:由(1)可知∠AFM=90°,
∴AF⊥FM
(3)
结论:∠BAM=22.5时,∠FMN=∠BAM
理由:
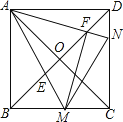
∵A、B、M、F四点共圆,
∴∠BAM=∠EFM,
∵∠BAM=∠FMN,
∴∠EFM=∠FMN,
∴MN∥BD,
∴ ![]() ,∵CB=DC,
,∵CB=DC,
∴CM=CN,
∴MB=DN,
在△ABM和△ADN中,
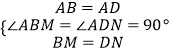 ,
,
∴△ABM≌△ADN,
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠BAM=22.5°.
【解析】(1)先证明A、B、M、F四点共圆,根据圆内接四边形对角互补即可证明∠AFM=90°,根据等腰直角三角形性质即可解决问题.(2)由(1)的结论即可证明.(3)由:A、B、M、F四点共圆,推出∠BAM=∠EFM,因为∠BAM=∠FMN,所以∠EFM=∠FMN,推出MN∥BD,得到 ![]() ,推出BM=DN,再证明△ABM≌△ADN即可解决问题.本题考查四边形综合题、等腰直角三角形性质、四点共圆、全等三角形的判定和性质等知识,解题的关键是利用四点共圆的性质解决问题,题目有点难,用到四点共圆.
,推出BM=DN,再证明△ABM≌△ADN即可解决问题.本题考查四边形综合题、等腰直角三角形性质、四点共圆、全等三角形的判定和性质等知识,解题的关键是利用四点共圆的性质解决问题,题目有点难,用到四点共圆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,车上原有(5a﹣2b)人,中途停车一次,有一些人下车,此时下车的人数比车上原有人数一半还多2人,同时又有一些上车,上车的人数比
 (7a﹣4b)少3人.
(7a﹣4b)少3人. (1)用代数式表示中途下车的人数;
(2)用代数式表示中途下车、上车之后,车上现在共有多少人?
(3)当a=10,b=9时,求中途下车、上车之后,车上现在的人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.

(1)求证:AE=AF;
(2)求证:BE= (AB+AC).
(AB+AC). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,
 ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为
),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为  .
.
(1)求a的值;
(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;
(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF. -
科目: 来源: 题型:
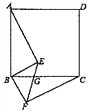
查看答案和解析>>【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
-
科目: 来源: 题型:
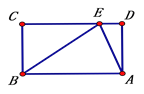
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,BC=6,点E为CD边上一点。
(1)当AE平分∠BED时,求DE的长。
(2)你能把矩形ABCD沿某条直线剪一刀分成两块,再拼成一个菱形吗?如果能,在备用图中画出示意图,并计算菱形较长对角线的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=6cm,BC=4 cm,E为CD中点.点P从A点出发,沿A—B—C的方向在矩形边上匀速运动,速度为1 cm /s,运动到C点停止.设点P运动的时间为t s.(图2为备用图)
(1)当P在AB上,t为何值时,△APE的面积是矩形ABCD面积的
 ?
?(2)在整个运动过程中,t为何值时,△APE为等腰三角形?

相关试题

