【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
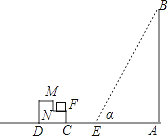
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
参考答案:
【答案】(1)15米;(2)小猫不能晒到太阳.
【解析】试题分析:(1)在Rt△ABE中,由tan56.3°=![]() ,即可求出AB=10tan56.3°,进而得出答案;
,即可求出AB=10tan56.3°,进而得出答案;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点P,与MC的交点为点Q,由∠BPA=45°,可得HQ=PH=0.3m,进而判断即可.
试题解析:(1)当α=56.3°时,在Rt△ABE中, ∵tan56.3°=![]() ≈1.50,
≈1.50,
∴AB=10tan56.3°≈10×1.50=15(m),
即楼房的高度约为15米;
(2)当α=45°时,小猫不能再晒到太阳,理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD交于点P,此时的影长AP=AB≈15m,
设MN的延长线交AD于点H,
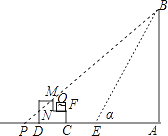
∵AC≈14.5m,NF=0.2m,
∴PH=AP﹣AC﹣CH≈15﹣14.5﹣0.2=0.3(m),
设直线MN与BP交于点Q,则HQ=PH=0.3m,
∴HQ=PH=0.3m,
∴点Q在MN上,
∴大楼的影子落在MN这个侧面上,
∴小猫不能晒到太阳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)解下列不等式(组),并把它们的解集在数轴上表示出来;
(1)
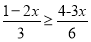 ; (2)
; (2)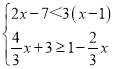
(Ⅱ)解方程组
(1)
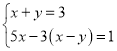 ; (2)
; (2)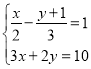 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B…依此类推,则平行四边形AO2019C2020B的面积为( )cm2.

A.
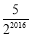 B.
B. 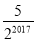 C.
C.  D.
D. 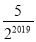
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(﹣15)﹣(﹣23)﹣(+35)+117
(2)(﹣1
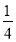 )×
)×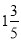 ÷(﹣0.25)
÷(﹣0.25)(3)
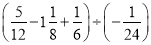
(4)﹣24﹣(﹣9)÷
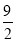 ×(﹣
×(﹣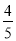 )×|﹣5|
)×|﹣5| -
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+
x+ 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
A. 2B. 4C. 6D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB、AC 交于 E、F 两点.下列结论:① BE+CF=
 BC;② S△AEF ≤
BC;② S△AEF ≤ S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )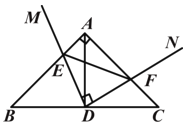
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

