【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.

(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动3.5秒时,求出点P的坐标;
(3)在移动过程中,若点P到x轴的距离为4个单位长度时,求点P移动的时间.
参考答案:
【答案】(1)4;6;(4,6);(2)(1,6);(3)点P移动的时间为2秒或6秒.
【解析】
(1)根据![]() +|b﹣6|=0、算术平方根的非负性及绝对值的非负性即可求出a和b,从而求出B的坐标;
+|b﹣6|=0、算术平方根的非负性及绝对值的非负性即可求出a和b,从而求出B的坐标;
(2)根据P点的速度和时间,即可求出P移动的路程,从而判断出P点所在的边,然后计算P点坐标即可;
(3)根据P到x轴的距离为4个单位长度,分类讨论即可.
解:(1)由题意得,a﹣4=0,b﹣6=0,
解得,a=4,b=6,
∴OA=4,OB=6,
∵四边形OABC为长方形,
∴点B的坐标为(4,6),
故答案为:4;6;(4,6);
(2)∵点P的速度是每秒2个单位长度,
∴点P移动3.5秒时,移动的距离为:3.5×2=7,而6<7<10
故此时P点在CB上
∴CP=7﹣6=1,且P点纵坐标为6.
∴点P的坐标(1,6);
(3)当点P在OC上时,
∵点P到x轴的距离为4个单位长度
∴此时移动的路程为4,
∴移动的时间为:4÷2=2(秒);
当点P在BA上时,
∴此时移动的路程为6+4+6﹣4=12,
∴移动的时间为:12÷2=6(秒),
综上所述,点P到x轴的距离为4个单位长度时,点P移动的时间为2秒或6秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2﹣EA2=AC2.

(1)求证:∠A=90°;
(2)若AB=8,BC=10,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x与反比例函数y=
 (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=
 (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.

(1)求∠DAD′的度数。
(2)当∠DAE=45°时,求证:DE=D′E;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,DE∥AB,EF∥AB,∠BED=∠CEF,
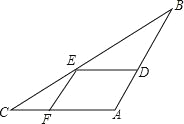
(1)试说明△ABC是等腰三角形,
(2)探索AB+AC与四边形ADEF的周长关系.
相关试题

