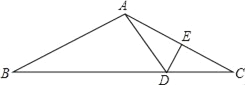
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.
(1)若AC=12,BC=15,求△ABD的周长;
(2)若∠B=20°,求∠BAD的度数.
参考答案:
【答案】(1)27;(2)120°.
【解析】
试题(1)根据线段垂直平分线性质求出AD=DC,求出△ABD周长=AB+BC即可;
(2)根据等腰三角形性质求出∠C,∠DAC,根据三角形内角和定理求出∠BAC,即可求出答案.
试题解析:(1)∵AC的垂直平分线分别交BC、AC于点D、E,
∴AD=DC,
∵AB=AC=12,
∴△ABD的周长为AB+AD+BD=AB+DC+BD=AB+BC=12+15=27;
(2)∵AB=AC,∠B=20°,
∴∠C=∠B=20°,
∴∠BAC=180°-20°-20°=140°,
∵AD=DC,
∴∠DAC=∠C=20°,
∴∠BAD=∠BAC-∠DAC=140°-20°=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数
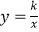 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) 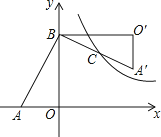
A.3
B.4
C.6
D.8 -
科目: 来源: 题型:
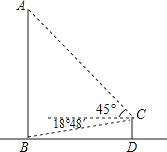
查看答案和解析>>【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为米(参考数据:tan78°12′≈4.8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.(1)作
 的平分线
的平分线 .
.(2)在
 上取一点
上取一点 ,使得
,使得 .
.(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现 与
与 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF =AD;
(2)若AD=2,AB=8,当BC为多少时,点B在线段AF的垂直平分线上?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察推理:如图①,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l的同侧,,垂足分别为.求证:△AEC≌△CDB.
(2)类比探究:如图②,在Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB,,连接CB,,求△ACB,的面积.
(3)拓展提升:如图③,在△EBC中,∠E=∠ECB=60°,EC=BC=3,点O在BC上,且OC=2,动点P从点E沿射线EC以每秒1个单位长度的速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点 F恰好落在射线EB上,求点P运动的时间t.

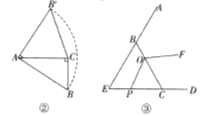
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
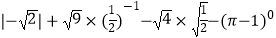 .
.
相关试题

