【题目】如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( ) 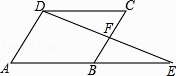
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
参考答案:
【答案】D
【解析】解:∵四边形ABCD是平行四边形, ∴CD//AB,
∴∠E=∠CDF,(故A成立);
∵四边形ABCD是平行四边形,
∴CD=AB,CD//BE,
∴∠C=∠CBE,
∵BE=AB,
∴CD=EB,
在△CDF和△BEF中,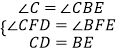 ,
,
∴△DCF≌△EBF(AAS),
∴EF=DF,(故B成立);
∵△DCF≌△EBF,
∴CF=BF= ![]() BC,
BC,
∵AD=BC,
∴AD=2BF,(故C成立);
∵AD≠BE,
∴2CF≠BE,(故D不成立);
故选:D.
首先根据平行四边形的性质可得CD//AB,再根据平行线的性质可得∠E=∠CDF;首先证明△DCF≌△EBF可得EF=DF;根据全等可得CF=BF= ![]() BC,再利用等量代换可得AD=2BF;根据题意不能证明AD=BE,因此BE不一定等于2CF.
BC,再利用等量代换可得AD=2BF;根据题意不能证明AD=BE,因此BE不一定等于2CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25

(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心,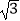 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
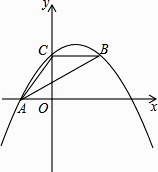
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(﹣3,0),与y轴交点为B,且与正比例函数y=
 x的图象交于点C(m,4).
x的图象交于点C(m,4).(1)求m的值及一次函数y=kx+b的表达式;
(2)观察函数图象,直接写出关于x的不等式
 x<kx+b的解集.
x<kx+b的解集.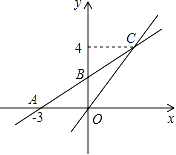
-
科目: 来源: 题型:
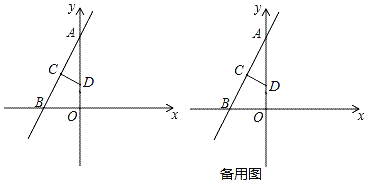
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,8),B(﹣4,0),线段AB的垂直平分线CD分别交AB、OA于点C、D,其中点D的坐标为(0,3).
(1)求直线AB的解析式;
(2)求线段CD的长;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式
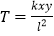 (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)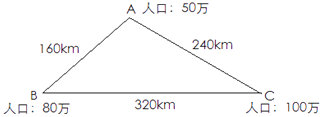
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
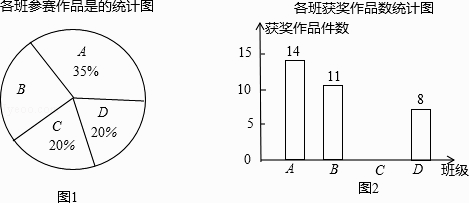
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
相关试题

