【题目】如图,抛物线y= ![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)解:把点A(0,﹣6)、B(﹣2,0)代入抛物线y= ![]() x2+bx+c中得:
x2+bx+c中得:
![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为:y= ![]() x2﹣2x﹣6;
x2﹣2x﹣6;
(2)解:y= ![]() x2﹣2x﹣6,
x2﹣2x﹣6,
当y=0时, ![]() x2﹣2x﹣6=0,
x2﹣2x﹣6=0,
解得:x1=﹣2,x2=6,
∴C(6,0);
设直线AC的解析式为:y=kx+b,
则 ![]() ,
,
解得: ![]() ,
,
∴直线AC的解析式为:y=x﹣6,
直线AC向下平移m个单位后的直线关系式为:y=x﹣6﹣m,
∵平移后的直线与抛物线有且只有一个公共点M,
则 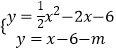 ,
,
得: ![]() =0,
=0,
△=(﹣3)2﹣4× ![]() m=0,
m=0,
m= ![]() ,
,
代入得:y=x﹣6﹣m=x﹣ ![]() ,
,
则 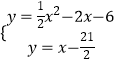 ,
,
解得: 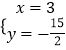 ,
,
∴M(3,﹣ ![]() );
);
(3)解:分三种情况:
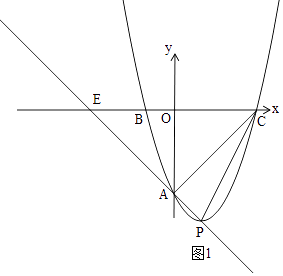
①当∠PAC=90°时,如图1,
∵OA=OC=6,∠AOC=90°,
∴△AOC是等腰直角三角形,
∴∠ACO=45°,
∴△EAC是等腰直角三角形,
∴AE=AC,
∴OE=OC=6,
∴E(﹣6,0),
设AE:y=kx+b,
则 ![]() ,解得:
,解得: ![]() ,
,
∴直线AE的解析式为:y=﹣x﹣6,
则 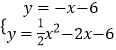 ,
,
![]() ﹣2x﹣6=﹣x﹣6,
﹣2x﹣6=﹣x﹣6,
解得:x1=0(舍),x2=2,
∴P(2,﹣8),
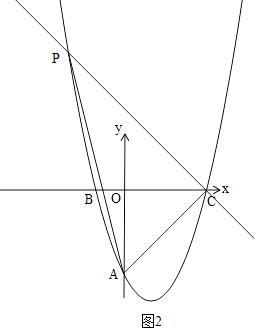
②当∠ACP=90°时,如图2,
∠PCB=90°﹣45°=45°,
过P作PE⊥BC于E,
∴△PEC是等腰直角三角形,
∴PE=EC,
设P(x, ![]() x2﹣2x﹣6),
x2﹣2x﹣6),
∴PE= ![]() x2﹣2x﹣6,EC=﹣x﹣6,
x2﹣2x﹣6,EC=﹣x﹣6,
∴ ![]() x2﹣2x﹣6=﹣x﹣6,
x2﹣2x﹣6=﹣x﹣6,
解得:x1=6,x2=﹣4,
∵P在第二象限,
∴x=6不符合题意,舍去,x=﹣4,
∴P(﹣4,10),
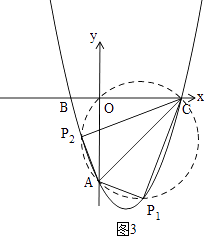
③以AC为直径画圆,交抛物线于两点P1、P2,如图3,
则∠AP1C=∠AP2C=90°,
∵ ![]() =
= ![]() ,
,
![]() =
= ![]() ,
,
AC2=62+62=72,
由勾股定理得: ![]() +
+ ![]() =72,
=72,
化简得:x3﹣8x2+8x+24=0,
x3﹣2x2﹣4x﹣(6x2﹣12x﹣24)=0,
x(x2﹣2x﹣4)﹣6(x2﹣2x﹣4)=0,
(x﹣6)(x2﹣2x﹣4)=0,
解得:x1=6(舍),x2=1+ ![]() ,x3=1﹣
,x3=1﹣ ![]() ,
,
∴P(1+ ![]() ,﹣5﹣
,﹣5﹣ ![]() )或(1﹣
)或(1﹣ ![]() ,﹣5+
,﹣5+ ![]() ),
),
综上所述,△PAC为直角三角形时,点P的坐标为:(2,﹣8),(﹣4,10),(1+ ![]() ,﹣5﹣
,﹣5﹣ ![]() ),(1﹣
),(1﹣ ![]() ,﹣5+
,﹣5+ ![]() ).
).
【解析】(1)利用待定系数法求二次函数的解析式;(2)由直线向下平移m个单位得:y=x﹣6﹣m,由直线与抛物线有且只有一个公共点M可知:由解析式列方程组根据△=0,可得结论;(3)分三种情况:①当∠PAC=90°时,如图1,由△EAC是等腰直角三角形,可得E(﹣6,0),直线AP与抛物线的交点就是P,列方程组可得P的坐标;②当∠ACP=90°时,如图2,由PE=EC,列式: ![]() x2﹣2x﹣6=﹣x﹣6,解出即可;③当APC=90°时,如图3,画圆,根据直径所对的圆周角是直角可知,有两个点符合,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标.
x2﹣2x﹣6=﹣x﹣6,解出即可;③当APC=90°时,如图3,画圆,根据直径所对的圆周角是直角可知,有两个点符合,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目
频数
频率
篮球
30
0.25
羽毛球
m
0.20
乒乓球
36
n
跳绳
18
0.15
其他
12
0.10
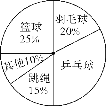
请根据以上图表信息,解答下列问题:
(1)频数分布表中的m=_________,n=_________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”
 为了便于记忆,同学们可仿照图用双手表示“三线八角”
为了便于记忆,同学们可仿照图用双手表示“三线八角” 两大拇指代表被截直线,食指代表截线
两大拇指代表被截直线,食指代表截线 下列三幅图依次表示
下列三幅图依次表示


A. 同位角、同旁内角、内错角B. 同位角、内错角、同旁内角
C. 同位角、对顶角、同旁内角D. 同位角、内错角、对顶角
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解黔东南州某县2016届中考学生的体育考试得分情况,从该县参加体育考试的4 000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数直方图.
成绩分组
频数
25≤x<30
4
30≤x<35
m
35≤x<40
24
40≤x<45
36
45≤x<50
n
50≤x<55
4

(1)求m,n的值,并补全频数直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀的学生人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3 000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x/分
频数/人
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25

根据所给信息,解答下列问题:
(1)m=_________,n=_________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在_________分数段;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )
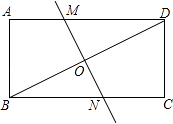
A.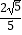
B.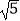
C.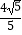
D.2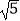
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 .
.
其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个
相关试题

