【题目】如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( ) 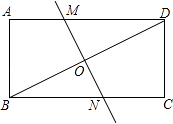
A.![]()
B.![]()
C.![]()
D.2 ![]()
参考答案:
【答案】B
【解析】解:如图,连接BM,DN
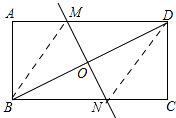
在矩形纸片ABCD中,CD=AB=2,∠C=90°,
在Rt△BCD中,BC=4,
根据勾股定理得,BD= ![]() =2
=2 ![]() ,
,
∴OB= ![]() BD=
BD= ![]() ,
,
由折叠得,∠BON=90°,ON= ![]() MN,BN=DN,
MN,BN=DN,
∵BC=BN+CN=4,
∴CN=4﹣BN,
在Rt△CDN中,CD=2,
根据勾股定理得,CN2+CD2=DN2,
(4﹣BN)2+22=BN2,
∴BN= ![]() ,
,
在Rt△BON中,ON= ![]() =
= ![]() ,
,
∴MN=2ON= ![]() ,
,
故选B.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解黔东南州某县2016届中考学生的体育考试得分情况,从该县参加体育考试的4 000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数直方图.
成绩分组
频数
25≤x<30
4
30≤x<35
m
35≤x<40
24
40≤x<45
36
45≤x<50
n
50≤x<55
4

(1)求m,n的值,并补全频数直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀的学生人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3 000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x/分
频数/人
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25

根据所给信息,解答下列问题:
(1)m=_________,n=_________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在_________分数段;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 .
.
其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点
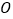 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到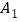 (0,1),
(0,1),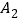 (1,1),
(1,1), (1,0),
(1,0),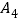 (2,0),…那么点
(2,0),…那么点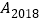 的坐标为__________.
的坐标为__________.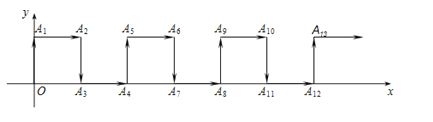
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
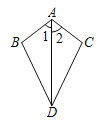
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
相关试题

