【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.

(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.
(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
试题解析:(1)∵ED与⊙O相切于D,∴OD⊥DE,∵F为弦AC中点,∴OD⊥AC,∴AC∥DE.
(2)作DM⊥OA于M,连接CD,CO,AD.
首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
∵AC∥DE,AE=AO,∴OF=DF,∵AF⊥DO,∴AD=AO,∴AD=AO=OD,∴△ADO是等边三角形,同理△CDO也是等边三角形,∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=a,∴AO∥CD,又AE=CD,∴四边形ACDE是平行四边形,易知DM=![]() ,∴平行四边形ACDE面积=
,∴平行四边形ACDE面积=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB=BC,对角线BD平分
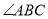 ,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.(1)求证:
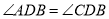 ;
;(2)若
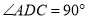 ,求证:四边形MPND是正方形。
,求证:四边形MPND是正方形。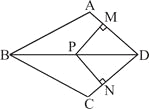
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x
···
1
2
3
5
7
9
···
y
···
1.98
3.95
2.63
1.58
1.13
0.88
···
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系
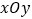 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;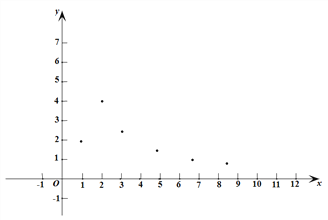
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N, 有下列四个结论:① DF=CF;② BF⊥EN;
③△BEN是等边三角形;④ S△BEF=3S△DEF.其中,正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数在数轴上所对应的点向右移动8个单位后,得到它的相反数,则这个数是( )
A. 4 B. -4 C. 8 D. -8
-
科目: 来源: 题型:
查看答案和解析>>【题目】x轴将坐标平面分为两部分,x轴上方的点的纵坐标为正数,x轴下方的点的纵坐标为______;y轴把坐标平面分为两部分,y轴左侧的点的横坐标为_____,y轴右侧的点的横坐标为_____.规定原点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个商店把某件商品按进价提高20%作为定价,可是总卖不出去;后来按定价减价20%出售,很快卖掉,结果这次生意亏了4元.那么这件商品的进价是________元.
相关试题

