【题目】已知如图,在菱形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
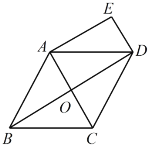
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析;(2)四边形AODE的面积为![]() .
.
【解析】
(1)先判断出四边形AODE是平行四边形,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据有一个角是直角的平行四边形是矩形可得结论;
(2)根据两直线平行,同旁内角互补求出∠ABC=60°,判断出△ABC是等边三角形,然后根据等边三角形的性质求出OA、OB,然后得到OD,再根据矩形的面积公式列式计算即可得解.
解:(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×6=3,OB=
×6=3,OB=![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=3×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;
……
如此进行下去,直至得C13.
若P(1,m)在C1上,则m =_________.
若P(37,n)在第13段抛物线C13上,则n =_________.

-
科目: 来源: 题型:
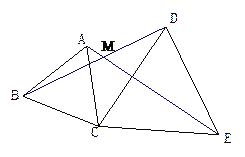
查看答案和解析>>【题目】如图,把△ACE绕点C逆时针旋转60°后与△BCD重合,BD、AE.交于点 M,连接AB、DE.
(1)求证:△ABC和△CDE为等边三角形;
(2)求∠AMB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为ACBD.上述结论正确的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
相关试题

