搜索
【题目】如图，在四边形ABCD中，AB=AD，BC=DC，AC与BD相交于点O，则①CA平分∠BCD；②AC⊥BD；③∠ABC=∠ADC=90°；④四边形ABCD的面积为ACBD．上述结论正确的个数是（ ）
A. 1个
B. 2个
C. 3个
D. 4个
参考答案：
【答案】B
【解析】
证明△ABC与△ADC全等，即可解决问题.
解：在△ABC与△ADC中，
，
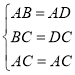∴△ABC≌△ADC（SSS），
∴∠ACB=∠ACD，故①正确，
∵AB=AD，BC=DC
∴AC是BD的垂直平分线，即AC⊥DB，
故②正确；
无法判断∠ABC=∠ADC=90°，故③错误，
四边形ABCD的面积=S△ADB+S△BCD=
DB×OA+DB×OC=ACBD，
故④错误；
故选：B．
-
科目： 来源： 题型：
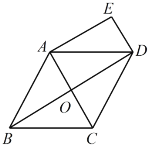
查看答案和解析>>【题目】已知如图，在菱形
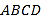中，对角线
，
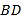相交于点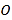
，
，
．
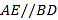（1）求证：四边形
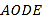是矩形；（2）若
，
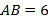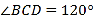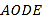，求四边形的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一段抛物线：y＝－x(x－3)（0≤x≤3），记为C1，它与x轴交于点O，A1；
将C1绕点A1旋转180°得C2，交x 轴于点A2；将C2绕点A2旋转180°得C3，交x 轴于点A3；
……
如此进行下去，直至得C13．
若P（1，m）在C1上，则m =_________．
若P（37，n）在第13段抛物线C13上，则n =_________．
-
科目： 来源： 题型：
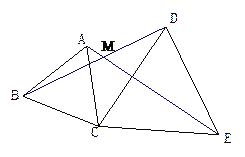
查看答案和解析>>【题目】如图，把△ACE绕点C逆时针旋转60°后与△BCD重合，BD、AE.交于点 M，连接AB、DE.
（1）求证：△ABC和△CDE为等边三角形；
（2）求∠AMB的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下面的解题过程的横线上填空，并在括号内注明理由。
如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.
解:∵∠A=∠F(已知)
∴DF∥AC(_____________________)
∴∠D=_____(______________________)
∵∠C=∠D(已知)
∴∠1=_____(___________________)
∴BD∥CE(_______________________)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线顶点D（-1，-4），且过点C（0，-3）.
（1）求此二次函数的解析式；
（2）抛物线与x轴交于点A、B，在抛物线上存在一点P使△ABP的面积为10，请直接写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形
的边长为
，点
从
开始沿折线
以
的速度移动，点
从
开始沿
边以
的速度移动，如果点，分别从，同时出发，当其中一点到达
时，另一点也随之停止运动．
（1）设
的面积为
，
为运动时间，写出关于的函数表达式；（2）
为何值时，的面积为正方形面积的
？
相关试题
