【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 . 
参考答案:
【答案】26
【解析】连接OA,AB⊥CD,

由垂径定理知,点E是AB的中点,AE= ![]() AB=5,OE=OC﹣CE=OA﹣CE,
AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,即r2=52+(r﹣1)2,
解得:r=13,所以CD=2r=26,即圆的直径为26.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
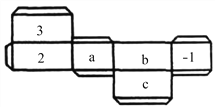
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)+4abc].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为
 ,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
A.(3,1)
B.(2,0)
C.(3,3)
D.(2,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(
 ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
ab+100)2+|a﹣20|=0,P是数轴上的一个动点.(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P能移动到与A或B重合的位置吗?若都不能,请直接回答.若能,请直接指出,第几次移动与哪一点重合.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学课上,老师要求学生根据图示张鑫与李亮的对话内容,展开如下活动:
活动1:仔细阅读对话内容

活动2:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,她需要付多少钱?
(2)你认为买多少元钱的书办卡就便宜?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.

(1)求证:△ABC∽△CBD;
(2)如果AC=4,BC=3,求BD的长.
相关试题

