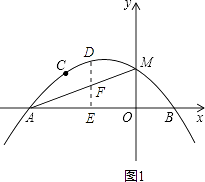
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
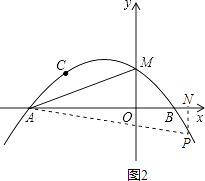
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:由题意可知 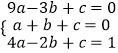 .解得
.解得 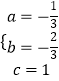 .
.
∴抛物线的表达式为y=﹣ ![]()
(2)解:将x=0代入抛物线表达式,得y=1.∴点M的坐标为(0,1).
设直线MA的表达式为y=kx+b,则 ![]() .
.
解得 ![]() .
.
∴直线MA的表达式为y= ![]() x+1.
x+1.
设点D的坐标为( ![]() ),则点F的坐标为(
),则点F的坐标为( ![]() ).
).
DF= ![]()
= ![]() .
.
当 ![]() 时,DF的最大值为
时,DF的最大值为 ![]() .
.
此时 ![]() ,即点D的坐标为(
,即点D的坐标为( ![]() )
)
(3)解:存在点P,使得以点P、A、N为顶点的三角形与△MAO相似.设P(m, ![]() ).
).
在Rt△MAO中,AO=3MO,要使两个三角形相似,由题意可知,点P不可能在第一象限.
①设点P在第二象限时,∵点P不可能在直线MN上,∴只能PN=3AN,
∴ ![]() ,即m2+11m+24=0.解得m=﹣3(舍去)或m=﹣8.又﹣3<m<0,故此时满足条件的点不存在.
,即m2+11m+24=0.解得m=﹣3(舍去)或m=﹣8.又﹣3<m<0,故此时满足条件的点不存在.
②当点P在第三象限时,∵点P不可能在直线MA上,∴只能PN=3AN,
∴ ![]() ,即m2+11m+24=0.
,即m2+11m+24=0.
解得m=﹣3或m=﹣8.此时点P的坐标为(﹣8,﹣15).
③当点P在第四象限时,若AN=3PN时,则﹣3 ![]() ,即m2+m﹣6=0.
,即m2+m﹣6=0.
解得m=﹣3(舍去)或m=2.
当m=2时, ![]() .此时点P的坐标为(2,﹣
.此时点P的坐标为(2,﹣ ![]() ).
).
若PN=3NA,则﹣ ![]() ,即m2﹣7m﹣30=0.
,即m2﹣7m﹣30=0.
解得m=﹣3(舍去)或m=10,此时点P的坐标为(10,﹣39).
综上所述,满足条件的点P的坐标为(﹣8,﹣15)、(2,﹣ ![]() )、(10,﹣39).
)、(10,﹣39).
【解析】(1)把点A、B、C的坐标分别代入已知抛物线的解析式列出关于系数的三元一次方程组 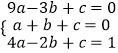 ,通过解该方程组即可求得系数的值;(2)由(1)中的抛物线解析式易求点M的坐标为(0,1).所以利用待定系数法即可求得直线AM的关系式为y=
,通过解该方程组即可求得系数的值;(2)由(1)中的抛物线解析式易求点M的坐标为(0,1).所以利用待定系数法即可求得直线AM的关系式为y= ![]() x+1.由题意设点D的坐标为(
x+1.由题意设点D的坐标为( ![]() ),则点F的坐标为(
),则点F的坐标为( ![]() ).易求DF=
).易求DF= ![]() =
= ![]() .根据二次函数最值的求法来求线段DF的最大值;(3)需要对点P的位置进行分类讨论:点P分别位于第一、二、三、四象限四种情况.此题主要利用相似三角形的对应边成比例进行解答.
.根据二次函数最值的求法来求线段DF的最大值;(3)需要对点P的位置进行分类讨论:点P分别位于第一、二、三、四象限四种情况.此题主要利用相似三角形的对应边成比例进行解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
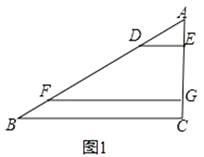
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= ,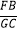 = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.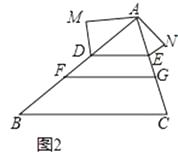
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.

(1)求a,b的值;
(2)连结OM,求∠AOM的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段
 、
、 、
、 ;
;求作:△ABC,使
 ,
,  ,
,  ;
;
【答案】答案见解析
【解析】试题分析:先画出与
 相等的角,再画出
相等的角,再画出 的长,连接
的长,连接 ,则
,则 即为所求三角形.
即为所求三角形.试题解析:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.

【题型】解答题
【结束】
15【题目】已知:线段
 ,
,  ,求作:
,求作:  ,使
,使 ,
,  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(
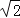 ≈1.414,精确到1米)
≈1.414,精确到1米)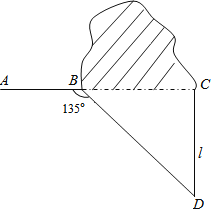
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
相关试题

