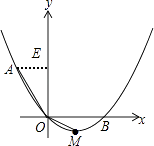
【题目】如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
(1)求a,b的值;
(2)连结OM,求∠AOM的大小.
参考答案:
【答案】
(1)解:如图,过点A作AE⊥y轴于点E,
∵AO=OB=2,∠AOB=120°,
∴∠AOE=30°,
∴AE=1,EO= ![]() ,
,
∴A点坐标为:(﹣1, ![]() ),B点坐标为:(2,0),
),B点坐标为:(2,0),
将两点代入y=ax2+bx得:
![]() ,
,
解得:  .
.
∴a= ![]() ,b=﹣
,b=﹣ ![]()
(2)解:由(1)可知:抛物线的表达式为:y= ![]() x2﹣
x2﹣ ![]() x;
x;

过点M作MF⊥OB于点F,
∵y= ![]() x2﹣
x2﹣ ![]() x=
x= ![]() (x2﹣2x)=
(x2﹣2x)= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() ,
,
∴M点坐标为:(1,﹣ ![]() ),
),
∴tan∠FOM= ![]() =
= ![]() ,
,
∴∠FOM=30°,
∴∠AOM=30°+120°=150°
【解析】(1)如图,过点A作AE⊥y轴于点E,根据含30°的直角三角形的边之间的关系得出AE,OE的长,进而得出A,B两点的坐标,然后利用待定系数法就可以求出a,b的值;
(2)过点M作MF⊥OB于点F,根据抛物线求出其顶点M的坐标,从而得出OF,MF的长度,根据tan∠FOM的值就可以求出∠FOM的值,进而得出答案。
-
科目: 来源: 题型:
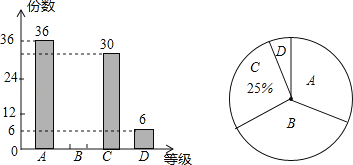
查看答案和解析>>【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.
(1)求抽取了多少份作品;
(2)此次抽取的作品中等级为B的作品有 ,并补全条形统计图;
(3)若该校共征集到800份作品,请估计等级为A的作品约有多少份.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 且平分
且平分 交
交 于点
于点 .①若
.①若 ,则
,则 _______;②若
_______;②若 ,则
,则 的周长为_____.
的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= ,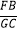 = .
= . 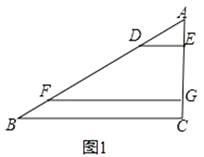
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.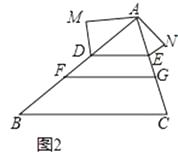
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.

(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段
 、
、 、
、 ;
;求作:△ABC,使
 ,
,  ,
,  ;
;
【答案】答案见解析
【解析】试题分析:先画出与
 相等的角,再画出
相等的角,再画出 的长,连接
的长,连接 ,则
,则 即为所求三角形.
即为所求三角形.试题解析:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.

【题型】解答题
【结束】
15【题目】已知:线段
 ,
,  ,求作:
,求作:  ,使
,使 ,
,  .
.
相关试题

