【题目】综合题
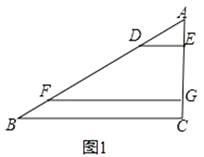
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , ![]() = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.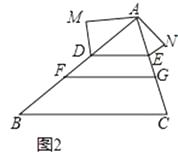
参考答案:
【答案】
(1)2,2
(2)证明:∵DE∥FG∥BC,
∴ ![]() ,
,
∵AM=BF,MD=DF,AN=GC,NE=EG,
∴ ![]() ,
,
∴△ADM∽△AEN,
∴∠M=∠N
【解析】(1)解:∵DE∥FG,
∴ ![]() ,
,
∵AD=2,AE=1,DF=4,
∴EG=2,
∴AF=AD+DF=6,AG=AE+EG=3,
∵DE∥FG∥BC,
∴ ![]() =2;
=2;
故答案为:2,2;
(1)根据平行线分线段成比例定理得出:AD∶DF=AE∶EG ,从而得出EG的长,进而得出AF,AG的长 ,再根据平行线分线段成比例定理得出FB∶GC=AF∶AG ,从而得出答案;
(2)根据平行线分线段成比例定理得出:AD∶AE=DF∶EG=FB∶GC ,又AM=BF,MD=DF,AN=GC,根据等量代换得出AD∶AE=MD∶NE=AM∶AN ,从而判断出△ADM∽△AEN,根据相似三角形对应角相等得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州地铁5号线全长48.18公里,投资315.9亿元,规划建设预期2014-2019年,杭州工程地铁队负责建设,分两个班组分别从杭州南站外香樟路站和余杭科技岛站同时开工掘进.已知甲组比乙组平均每天多掘进2.4米,经过5天施工,两组共掘进了110米.
(1)求甲、乙两个班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进1.7米,乙组平均每天能比原来多掘进1.3米.按此施工进度,能够比原来少用多少天完成任务?
-
科目: 来源: 题型:
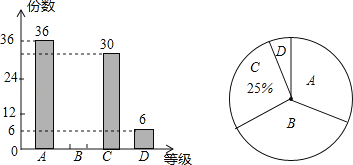
查看答案和解析>>【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.
(1)求抽取了多少份作品;
(2)此次抽取的作品中等级为B的作品有 ,并补全条形统计图;
(3)若该校共征集到800份作品,请估计等级为A的作品约有多少份.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 且平分
且平分 交
交 于点
于点 .①若
.①若 ,则
,则 _______;②若
_______;②若 ,则
,则 的周长为_____.
的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.

(1)求a,b的值;
(2)连结OM,求∠AOM的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.

(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
相关试题

