搜索
【题目】如图，M是线段AC中点，B在线段AC上，且AB=2cm、BC=2AB，求BM长度． 
参考答案：
【答案】解：∵AB=2cm，BC=2AB， ∴BC=4cm，
∴AC=AB+BC=2+4=6cm，
∵M是线段AC中点，
∴AM= 
AC=3cm，
∴BM=AM﹣AB=3﹣2=1cm．
故BM长度是1cm．
【解析】先根据AB=2cm，BC=2AB求出BC的长，进而得出AC的长，由M是线段AC中点求出AM，再由BM=AM﹣AB即可得出结论．
【考点精析】本题主要考查了两点间的距离的相关知识点，需要掌握同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记才能正确解答此题．
-
科目： 来源： 题型：
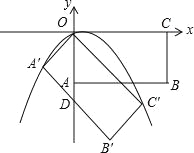
查看答案和解析>>【题目】如图，在平面直角坐标系中，矩形OABC的顶点O为坐标原点，顶点A、C的坐标分别为（0，﹣
）、（2，0），将矩形OABC绕点O顺时针旋转45°得到矩形OA′B′C′，边A′B′与y轴交于点D，经过坐标原点的抛物线y=ax2+bx同时经过点A′、C′．（1）求抛物线所对应的函数表达式；
（2）写出点B′的坐标；
（3）点P是边OC′上一点，过点P作PQ⊥OC′，交抛物线位于y轴右侧部分于点Q，连接OQ、DQ，设△ODQ的面积为S，当直线PQ将矩形OA′B′C′的面积分为1：3的两部分时，求S的值；
（4）保持矩形OA′B′C′不动，将矩形OABC沿射线CO方向以每秒1个单位长度的速度平移，设平移时间为t秒（t＞0）．当矩形OABC与矩形OA′B′C′重叠部分图形为轴对称多边形时，直接写出t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠A＞∠B．
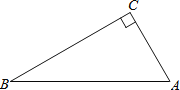
（1）用直尺和圆规作AB的垂直平分线，交AB与D，交BC于E；（不写作法，保留作图痕迹）
（2）在（1）的条件下，若CE=DE，求∠A，∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a是正数，则-a一定是（ ）.
A.正数
B.负数
C.正数或负数
D.正数或零或负数 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组量中，不是互为相反意义的量的是（ ）.
A.收入200元与支出20元
B.上升10米与下降7米
C.超过0.05米与不足0.03米
D.增大2岁与减少2升 -
科目： 来源： 题型：
查看答案和解析>>【题目】河南姑娘朱婷是一位非常优秀和被观众喜爱的排球运动员，下面一组数据是她在某系列赛中的得分统计（单位：分）：20，21，24，27，19，23，24，26，23，24，则此系列赛得分的众数和中位数分别是 （ ）
A.23，24B.23，23.5C.24，23D.24，23.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】经过以下一组点可以画出函数y＝2x图象的是()
A. (0，0)和(2，1) B. (0，0)和(1，2)
C. (1，2)和(2，1) D. (－1，2)和(1，2)
相关试题
