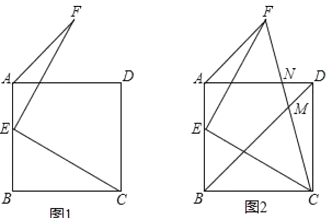
【题目】如图1,点![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,
上一点,![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求![]() 的度数;
的度数;
(2)如图2,连接![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
求证:![]() .
.
参考答案:
【答案】(1)135°;(2)见详解.
【解析】
(1)过点F作FM⊥AB交AB的延长线于点M,证明△EBC△FME,即可解决问题;
(2)过点F作FG//AB交BD于点G.先证明四边形ABGF为平行四边形,再证明△FGM△CDM,即可解决问题.
(1)过点F作FM⊥AB交AB的延长线于点M,
∵四边形ABCD是正方形,
∴∠B=∠M=∠CEF=90°,
∴∠MEF+∠CEB=90°,∠CEB+∠BCE=90°,
∴∠MEF=∠ECB,
∵EC=EF,
∴△EBC△FME(AAS) ,
∴FM=BE,EM=BC,
∵BC=AB,
∴EM=AB,
∴EMAE=ABAE,
∴AM=BE,
∴FM=AM,
∵FM⊥AB,
∴∠MAF=45°,
∴∠EAF=135°;
(2)过点F作FG//AB交BD于点G.
由(1)可知∠EAF=135°,
∵∠ABD=45°,
∴∠EAF+∠ABD=180°,
∴AF//BG,
∵FG//AB,
∴四边形ABGF为平行四边形,
∴AF=BG,FG=AB,
∵AB=CD,
∴FG=CD,
∵AB//CD,
∴FG//CD,
∴∠FGM=∠CDM,
∵∠FMG=∠CMD
∴△FGM△CDM(AAS),
∴GM=DM,
∴DG=2DM,
∴BD=BG+DG=AF+2DM.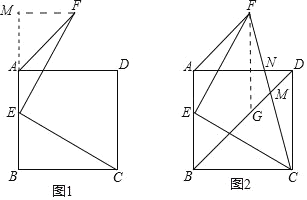
-
科目: 来源: 题型:
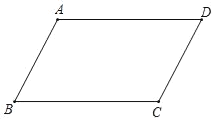
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AE⊥BD于点E,连接EC.
(1)依题意补全图形;
(2)在平面内找一点F,使得四边形ECFA是平行四边形,请在图中画出点F,叙述你的画图过程,并证明.
-
科目: 来源: 题型:
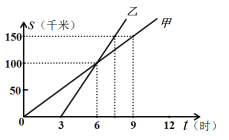
查看答案和解析>>【题目】如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,___________ 是自变量,___________ 是因变量.
(2)甲的速度 ___________ 乙的速度.(填“大于”、“等于”、或“小于”)
(3)甲与乙 ___________ 时相遇.
(4)甲比乙先走 ___________ 小时.
(5)9时甲在乙的 ___________ (填“前面”、“后面”、“相同位置”).
(6)路程为150km,甲行驶了___________ 小时,乙行驶了___________ 小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为
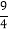 ,请直接写出点M的坐标.
,请直接写出点M的坐标.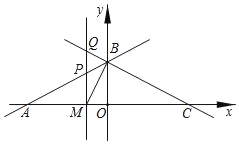
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小亮一家在东昌湖游玩,妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船(如图).小船从P处出发,沿北偏东60°划行200米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
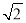 ≈1.41,
≈1.41,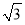 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
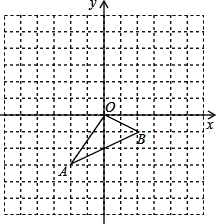
查看答案和解析>>【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=4,AD是BC边上的中线,将△ABD绕点A旋转,使AB与AC重合,连接DE,则线段DE的长为_____.

相关试题

