【题目】一辆货车从百货大楼出发负责送货,向东走了2千米到达小明家,继续向东走了4千米到达小红家,然后向西走了9千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.5升,那么这辆货车共耗油多少升?
参考答案:
【答案】(1)见解析;(2)5千米;(3)9升.
【解析】
(1)根据已知,以百货大楼为原点,以向东为正方向,用1个单位长度表示1千米一辆货车从百货大楼出发,向东走了2千米,到达小明家,继续向东走了4千米到达小红家,然后西走了9千米,到达小刚家,最后返回百货大楼,则小明家、小红家和小刚家在数轴上的位置可知.
(2)用小明家的坐标减去与小刚家的坐标即可.
(3)这辆货车一共行走的路程,实际上就是2+4+9+3=18(千米),货车从出发到结束行程共耗油量=货车行驶每千米耗油量×货车行驶所走的总路程.
解:(1)如图所示:
![]()
(2)由小明与小刚在数轴上的位置可得:![]() 千米
千米
(3)这辆货车此次送货共耗油:![]() 升
升
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的解题过程,再解决问题.
解方程: x4 -6x2 +5=0.
这是一个一元四次方程,根据该方程的特点,它的通常解法是:
设 x2 = y ,则原方程可化为 y2 -6y+5=0.①
解这个方程,得 y1 =1, y2 =5.当 y =1时, x=±1;当 y=5时, x=±
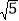 .所以原方程有四个根: x1 =1, x2 =-1, x3 =
.所以原方程有四个根: x1 =1, x2 =-1, x3 =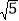 , x4 =-
, x4 =-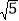 .
. (1)填空:在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了________的数学思想.
(2)解方程:( x2 -x )2 -4(x2 -x )-12=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠ABC=35°,E是BC边上一点且AE=CE,D是
BC边上的中点,连接AD,AE.
(1)求∠DAE的度数;
(2)若BD上存在点F,且∠AFE=∠AEF,求证:BF=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的部分图象如图所示,则关于
的部分图象如图所示,则关于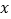 的一元二次方程
的一元二次方程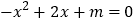 的解为 .
的解为 .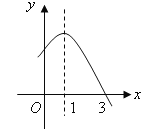
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a、b、c、d.

(1)若c与d互为相反数,则a________;
(2)若d2b8,那么点C对应的数是________;
(3)若abcd0,ab0求
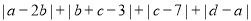 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点B是线段AD上一点,△ABC和△BDE分别是等边三角形,连接AE和CD.
(1)求证:AE=CD;
(2)如图2,点P、Q分别是AE、CD的中点,试判断△PBQ的形状,并证明.
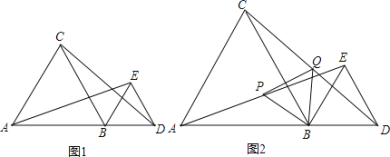
-
科目: 来源: 题型:
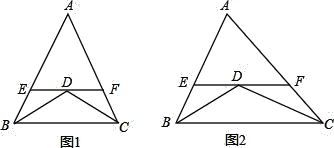
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
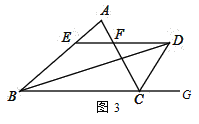
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
相关试题

