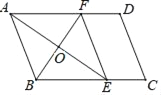
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于E,点F在AD上,且AF=AB,连接EF.
(1)判断四边形ABEF的形状并证明;
(2)若AE、BF相交于点O,且四边形ABEF的周长为20,BF=6,求AE的长度及四边形ABEF的面积.
参考答案:
【答案】(1)四边形ABEF是菱形;理由见解析;(2)AE=8;四边形ABEF的面积是24.
【解析】
(1)由平行四边形的性质和角平分线得出∠BAE=∠AEB,证出BE=AB,由AF=AB
得出BE=AF,即可得出结论.
(2)根据菱形的性质可得AE⊥BF,BO=![]() FB=3,AE=2AO,利用勾股定理计算出AO的
FB=3,AE=2AO,利用勾股定理计算出AO的
长,进而可得AE的长.菱形的面积=对角线乘积的一半.
(1)四边形ABEF是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形;
(2)∵四边形ABEF为菱形,
∴AE⊥BF,BO=![]() FB=3,AE=2AO,
FB=3,AE=2AO,
在Rt△AOB中,![]()
∴AE=2AO=8.
∴四边形ABEF的面积为:![]()
综上所述,AE=8;四边形ABEF的面积是24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的方格形中,点A、B、C在小正方形的顶点上.在BC上找一点P,使点P到AB和AC的距离相等.
实验与操作:
(1)在BC上找一点P,使点P到AB和AC的距离相等;
(2)在射线AP上找到一点Q,使QB=QC.
探索与计算:
如果A点坐标为(-1,-3),
(1)试在图中建立平面直角坐标系;
(2)若点M、N是坐标系中小正方形的顶点,且四边形QCMN是一个正方形,则 M点的坐标是__________,N点的坐标是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①
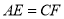 ;②
;②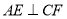 .
.(2)若
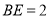 ,
,① 如图2,点E在正方形内,连接EC,若
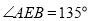 ,
, 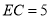 ,求
,求 的长;
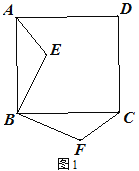
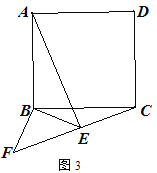
的长;② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l1:y=﹣
 x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=3MN时,求t的值;
②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2018的坐标是( )

A. (5,3) B. (3,5) C. (0,2) D. (2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2011年5月19日,中国首个旅游日正式启动.某校组织了八年级800名学生参加的旅游地理知识竞赛,李老师为了了解学生对旅游地理知识的掌握情况,从中随机抽取了部分学生的成绩作为样本,把成绩按优秀、良好、及格和不及格4个级别进行统计,并绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
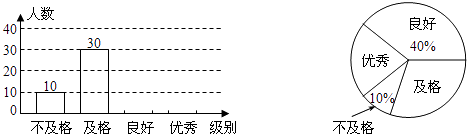
请根据以上提供的信息,解答下列问题:
(1)求被抽取部分学生的人数;
(2)请补全条形统计图,并求出扇形统计图中表示及格的扇形的圆心角度数;
(3)请估计八年级800名学生中达到良好和优秀的总人数.
相关试题

